Aprendizaje Automático sobre
Grandes Volúmenes de Datos
Clase 11
Pablo Ariel Duboue, PhD
Universidad Nacional de Córdoba,
Facultad de Matemática, Astronomía y Física

None.1 Undécima Clase: Operaciones Matriciales Distribuidas
None.1.1 Clase anterior
Material de lectura
-
Clase pasada:
-
Brewer’s conjecture and the feasibility of consistent, available, partition-tolerant web services por S Gilbert, N Lynch
- ACM SIGACT News, 2002
-
CAP twelve years later: How the" rules" have changed por E Brewer
- Computer, 2012
- http://en.wikipedia.org/wiki/Fallacies_of_Distributed_Computing
-
Brewer’s conjecture and the feasibility of consistent, available, partition-tolerant web services por S Gilbert, N Lynch
-
Ésta clase:
- Capítulo 6 del Owen et al. (2012)
- http://www.cs.utah.edu/~jeffp/teaching/cs7960/L17-MR-Matrix+DB
-
Scalable Scientific Computing Algorithms Using MapReduce por Xiang Jingen, Master of Mathematics, CS School, UWaterloo 2013
- https://uwspace.uwaterloo.ca/bitstream/handle/10012/7830/Xiang_Jingen.pdf
-
HAMA: An efficient matrix computation with the mapreduce framework por Seo, S., Yoon, E. J., Kim, J., Jin, S., Kim, J. S., & Maeng, S
- CloudCom, 2010
Preguntas
-
¿Qué tipo de decisiones CAP hace hadoop?
- Pierde Disponibilidad
-
CAP parece más orientado a datos que a cómputo:
- En realidad los datos se refiere a un cierto "estado global" o compartido
-
Un problema que afecta cualquier tipo de programa con estado (excepto programación funcional perezosa)
- Bases de datos, sistemas de archivos distribuidos, etc
- Por eso las bases NoSQL no soportan ACID
-
¿Hay contextos prácticos donde no import Consistencia o Disponibilidad?
- Falta de consistencia: decoraciones, datos de menor importancia
- Falta de disponibilidad: proceso por lotes
- Java para pythoneros (lista)
- Preguntas sobre el práctico y su actualización
Recordatorio
-
El sitio Web de la materia es http://aprendizajengrande.net
- Allí está el material del curso (filminas, audio)
-
Leer la cuenta de Twitter https://twitter.com/aprendengrande es obligatorio antes de venir a clase
- Allí encontrarán anuncios como cambios de aula, etc
- No necesitan tener cuenta de Twitter para ver los anuncios, simplemente visiten la página
-
Suscribirse a la lista de mail en aprendizajengrande@librelist.com es optativo
- Si están suscriptos a la lista no necesitan ver Twitter
-
Feedback para alumnos de posgrado es obligatorio y firmado, incluyan si son alumnos de grado, posgrado u oyentes
- El "resúmen" de la clase puede ser tan sencillo como un listado del título de los temas tratados
Las 8 falacias del cómputo distribuido
-
Todo programador comete alguno de estos errores cuando empieza cómputo distribuido (L. Peter Deutsch y otros):
- La red es confiable
- Hay cero latencia
- El ancho de banda es infinito
- La red es segura
- La topología no cambia
- Hay un sólo administrador
- El costo de transporte es cero
- La red es homogénea
Revisión CAP
-
Cuando estamos en un ambiente distribuido, de estas tres características sólo podes escoger dos:
- Consistencia
- Disponibilidad (Availability)
- Tolerancia a particiones de la red (Partition-tolerance)
Teorema CAP asíncrono
Dado el modelo de cómputo asíncrono, no es posible garantizar Consistencia y Disponibilidad
Demostración:
-
por el absurdo, se construye una cadena de ejecución que actualiza un valor v en un nodo y se pierden los mensajes de actualización en el otro
- cuando se pide el valor de v en el otro nodo, por Disponibilidad el otro nodo tiene que responder y responde con el valor equivocado
Corolario:
- Tampoco se puede garantizar Consistencia y Disponibilidad aún cuando no se pierdan mensajes (pero se puedan demorar lo suficiente como para que se de la construcción por el absurdo del teorema).
Teorema CAP revisitado
-
Formalización clásica ignora el concepto de latencia, pero es clave.
-
Durante un time-out, el programa debe decidir:
- cancelar la operación (afecta Disponibilidad)
- continuar la operación (afecta Consistencia)
- Continuar re-intentando es elegir Consistencia en vez de Disponiblidad
-
Durante un time-out, el programa debe decidir:
-
También está la cuestión práctica... es posible realmente elegir Consistencia+Disponibilidad? Tarde o temprano la red fallará
- Interpretación probabilística de C, A y P
- Nuevo énfasis en recuperación después de particiones
None.1.2 Aplicaciones Matriciales Distribuidas
Distribución de Matrices Dispersas
- Según el tipo de operación, distribuimos filas o columnas
- Si una fila o columna no entra en un solo nodo, distribuimos franjas de filas o columnas
Multiplicación de una matriz por un vector
Ax = ⎡⎢⎢⎢⎢⎢⎣
a11
a12
…
a1n
a21
a22
…
a2n
⋮
⋮
⋮
⋮
am1
am2
…
amn
⎤⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎣
x1
x2
⋮
xn
⎤⎥⎥⎥⎥⎥⎦ = ⎡⎢⎢⎢⎢⎢⎣
a11x1 + a12x2 + ⋯ + a1nxn
a21x1 + a22x2 + ⋯ + a2nxn
⋮
am1x1 + am2x2 + ⋯ + amnxn
⎤⎥⎥⎥⎥⎥⎦
http://mathinsight.org/matrix_vector_multiplication
Matriz por vector en MR
- Entrada: Matriz M = n × n, vector V = n × 1
-
Salida: Vector X = M*V
- xi = ∑nj = 1mij*vj
-
Map(i, <fila i de M, V >):
- (j,mij*vj)
-
Reduce(j,mij*vj):
- xi = ∑nj = 1mijvj
- Si V no entra en un mapper, distribuir franjas de V a cada mapper
Multiplicación de Matriz por Matriz
⎡⎢⎢⎢⎢⎢⎣
b11
b12
…
b1p
b21
b22
…
b2p
⋮
⋮
⋮
⋮
bn1
bn2
…
bnp
⎤⎥⎥⎥⎥⎥⎦ = ⎡⎢⎢⎢⎢⎢⎣⎡⎢⎢⎢⎢⎢⎣
b11
b21
⋮
bn1
⎤⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎣
b12
b22
⋮
bn2
⎤⎥⎥⎥⎥⎥⎦⋯⎡⎢⎢⎢⎢⎢⎣
b1p
b2p
⋮
bnp
⎤⎥⎥⎥⎥⎥⎦⎤⎥⎥⎥⎥⎥⎦
http://mathinsight.org/matrix_vector_multiplication
Matriz por Matriz dispersa
- Una concatenación de los vectores obtenidos de multiplicar las columnas de la segunda matriz por la primera
- La clave recibida en el mapper es una clave compuesta y recibe la fila y la columna sobre la que se está operando
-
Map((i, k), <fila i de M, columna k deB >):
- ((j, k),mij*njk)
- el índice de la columna final es el mismo que el de la columna en al segunda matriz
Multiplicación de Matrices Densas
- División por bloques
- La multiplicación de un bloque por el otro entra en la memoria de cada nodo
- HAMA
Álgebra Relacional
- Para matrices booleanas es posible implementar unión e intersección en MR
- Muy similar al ejemplo de conteo de palabras
Solución de Ax = b
- Dados una matriz A simétrica y definida positiva y un vector B, buscamos un vector x tal que Ax = b
-
Método del gradiente conjugado:
- Definimos f(x) = (1)/(2)xTAx − bTx + c
- Entonces f’(x) = (1)/(2)ATx + (1)/(2)Ax − b = Ax − b
- La ecuación Ax = b tiene un cero en los puntos críticos de la ecuación de arriba
- Usamos el gradiente conjugado para decidir la dirección de búsqueda y una búsqueda lineal para optimizar el tamaño del paso en esa dirección
- Ver paper de HAMA para los detalles
Descomposición LU
-
A = LU
- Para mejorar la estabilidad numérica se suele usar una permutación P de A
- L es triangular inferior, U es triangular superior
- Las matrices triangulares son fáciles de invertir
Descomposición LU en MR
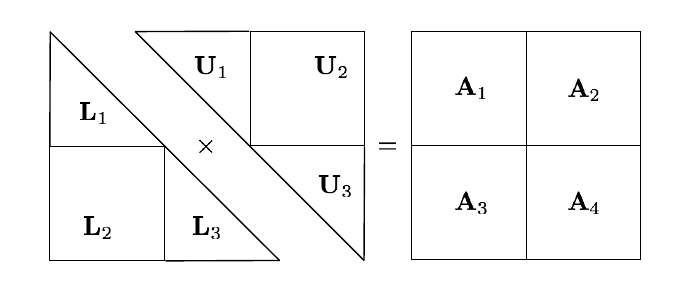
(adaptado de Xiang Jingen, 2013)