Aprendizaje Automático sobre
Grandes Volúmenes de Datos
Clase 12
Pablo Ariel Duboue, PhD
Universidad Nacional de Córdoba,
Facultad de Matemática, Astronomía y Física

None.1 Duodécima Clase: Descomposición LU distribuida
None.1.1 Clase anterior
Material de lectura
-
Clase pasada:
- Capítulo 6 del Owen et al. (2012)
- http://www.cs.utah.edu/~jeffp/teaching/cs7960/L17-MR-Matrix+DB
-
HAMA: An efficient matrix computation with the mapreduce framework por Seo, Yoon, Kim, Jin, Kim, Maeng
- CloudCom, 2010
-
Ésta clase:
-
Scalable Scientific Computing Algorithms Using MapReduce por Xiang Jingen, Master of Mathematics UWaterloo ’13
- https://uwspace.uwaterloo.ca/bitstream/handle/10012/7830/Xiang_Jingen.pdf
-
Design and Evaluation of Parallel Block Algorithms: LU Factorization on an IBM 3090 VF/600J, por Dackland, Elmroth, Kågström, Van Loan.
- 5th SIAM Conf. on Parallel Processing for Scientific Computing, 1991
- Parallelized stochastic gradient descent por Zinkevich, Weimer, Li, Smola (NIPS 2010)
-
Scalable Scientific Computing Algorithms Using MapReduce por Xiang Jingen, Master of Mathematics UWaterloo ’13
Preguntas
- Preguntas sobre LU (hoy)
-
Representaciones estándar
- HIVE
-
Ejemplo de Map/Reduce
- Próxima clase
-
Material de lectura previo
- Ahora en Twitter / Lista
- Metodología de evaluación
Recordatorio
-
El sitio Web de la materia es http://aprendizajengrande.net
- Allí está el material del curso (filminas, audio)
-
Leer la cuenta de Twitter https://twitter.com/aprendengrande es obligatorio antes de venir a clase
- Allí encontrarán anuncios como cambios de aula, etc
- No necesitan tener cuenta de Twitter para ver los anuncios, simplemente visiten la página
-
Suscribirse a la lista de mail en aprendizajengrande@librelist.com es optativo
- Si están suscriptos a la lista no necesitan ver Twitter
-
Feedback para alumnos de posgrado es obligatorio y firmado, incluyan si son alumnos de grado, posgrado u oyentes
- El "resúmen" de la clase puede ser tan sencillo como un listado del título de los temas tratados
Distribución de Matrices Dispersas
- Según el tipo de operación, distribuimos filas o columnas
- Si una fila o columna no entra en un solo nodo, distribuimos franjas de filas o columnas
Multiplicación de una matriz por un vector
Ax = ⎡⎢⎢⎢⎢⎢⎣
a11
a12
…
a1n
a21
a22
…
a2n
⋮
⋮
⋮
⋮
am1
am2
…
amn
⎤⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎣
x1
x2
⋮
xn
⎤⎥⎥⎥⎥⎥⎦ = ⎡⎢⎢⎢⎢⎢⎣
a11x1 + a12x2 + ⋯ + a1nxn
a21x1 + a22x2 + ⋯ + a2nxn
⋮
am1x1 + am2x2 + ⋯ + amnxn
⎤⎥⎥⎥⎥⎥⎦
http://mathinsight.org/matrix_vector_multiplication
Matriz por vector en MR
- Entrada: Matriz M = n × n, vector V = n × 1
-
Salida: Vector X = M*V
- xi = ∑nj = 1mij*vj
-
Map(i, <fila i de M, segmento de V entre bs y be>):
- (i,∑bej = bsmij*vj)
-
Reduce(i,∑bej = bsmij*vj):
- xi = ∑nj = 1mijvj
Multiplicación de Matriz por Matriz
⎡⎢⎢⎢⎢⎢⎣
b11
b12
…
b1p
b21
b22
…
b2p
⋮
⋮
⋮
⋮
bn1
bn2
…
bnp
⎤⎥⎥⎥⎥⎥⎦ = ⎡⎢⎢⎢⎢⎢⎣⎡⎢⎢⎢⎢⎢⎣
b11
b21
⋮
bn1
⎤⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎣
b12
b22
⋮
bn2
⎤⎥⎥⎥⎥⎥⎦⋯⎡⎢⎢⎢⎢⎢⎣
b1p
b2p
⋮
bnp
⎤⎥⎥⎥⎥⎥⎦⎤⎥⎥⎥⎥⎥⎦
http://mathinsight.org/matrix_vector_multiplication
Matriz por Matriz dispersa
- Una concatenación de los vectores obtenidos de multiplicar las columnas de la segunda matriz por la primera
- La clave recibida en el mapper es una clave compuesta y recibe la fila y la columna sobre la que se está operando
-
Map((i, k), <fila i de M, columna k deB >):
- ((i, k),∑nj = 1mij*njk)
- el índice de la columna final es el mismo que el de la columna en al segunda matriz
Solución de Ax = b
- Dados una matriz A simétrica y definida positiva y un vector B, buscamos un vector x tal que Ax = b
-
Método del gradiente conjugado:
- Definimos f(x) = (1)/(2)xTAx − bTx + c
- Entonces f’(x) = (1)/(2)ATx + (1)/(2)Ax − b = Ax − b
- La ecuación Ax = b tiene un cero en los puntos críticos de la ecuación de arriba
- Usamos el gradiente conjugado para decidir la dirección de búsqueda y una búsqueda lineal para optimizar el tamaño del paso en esa dirección
None.2 Descomposición LU distribuida
Temas Claves
- Identificación de la máxima tarea que puede hacerse por nodo
- Descomposición de la tarea normal en tareas por nodo
- Tareas globales, realizadas en un nodo (central) y tareas paralelas
- Comunicación entre tareas mediante HDFS y archivos bandera
- Tareas que sólo hacen Map
- Cálculos intermedios
Inversión Matricial
-
La inversa de una matriz A es otra matriz B tal que AB = BA = In donde In es la matriz identidad.
- La inversa de A se denota por A − 1
Algoritmos clásicos para encontrar la matriz inversa
-
Gauss-Jordan
- Realizar operaciones en órden
-
SVD, calcular U, V y W tales que
-
A = UWVT con
- UUT = VVT = In
- W diagonal
- Requiere intercambios de filas
-
A = UWVT con
-
Decomposición QR
-
A = QR con
- QQT = In
- R triangular superior
- Usa Gram-Schmidt para calcular vectores en órden
-
A = QR con
- Descomposición LU
Descomposición LU
-
A = LU
- Para mejorar la estabilidad numérica se suele usar una permutación P de A
- L es triangular inferior, U es triangular superior
- Las matrices triangulares son fáciles de invertir
Descomposición LU
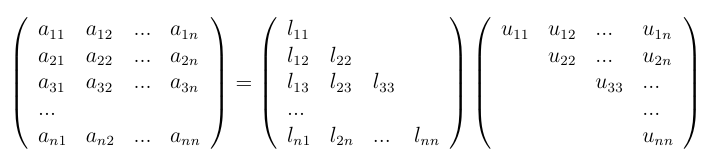
(adaptado de Xiang Jingen, 2013)
Descomposición LU
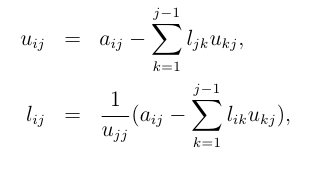
(adaptado de Xiang Jingen, 2013)
Descomposición LU en una máquina

(adaptado de Xiang Jingen, 2013)
Descomposición LU en MR
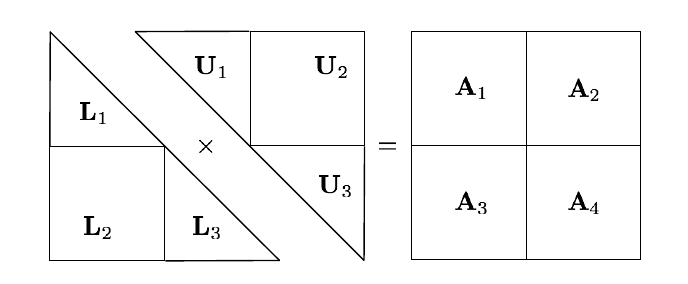
(adaptado de Xiang Jingen, 2013)
Descomposición LU en MR
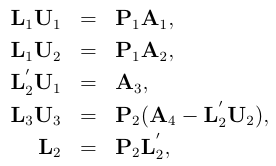
(adaptado de Xiang Jingen, 2013)
El algoritmo a vuelo de pájaro
- Dividir la matriz original recursivamente hasta que L1 U1 = P1 A1 sea soluble en una máquina
- Descomponer A1
- Calcular U2
- Calcular la permutación de L2, L’2
- Calcular B = A4 − L’2 U2
- Descomponer B
- Armar la salida total a partir las partes
El Algoritmo

(adaptado de Xiang Jingen, 2013)
Implementación en MapReduce
- Datos en archivos separados
- Ciertas partes de la matriz se guarda por filas, ciertas partes por columnas
-
Los resultados intermedios se concretizan en disco
- Mejor tolerancia a fallas
- Enlentece el algoritmo innecesariamente
- Restricción de Hadoop (Spark no tendría ese problema)
- Primera pasada recursiva genera archivos de control
- El resto del sistema opera a partir de esos archivos de control
- Tareas de sólo map
Implementación en MapReduce
-
Nodo master crea archivos de control que son usados como entrada a las tareas map subsecuentes
- Falsas entradas
- Una tarea MapReduce subdivide A de manera recursiva
-
Se envian tareas MapReduce para L’2, U2 y B
- L1 y U1 son ejecutadas en el master node si A1es lo suficientemente pequeña
Datos

(adaptado de Xiang Jingen, 2013)
Ejecución
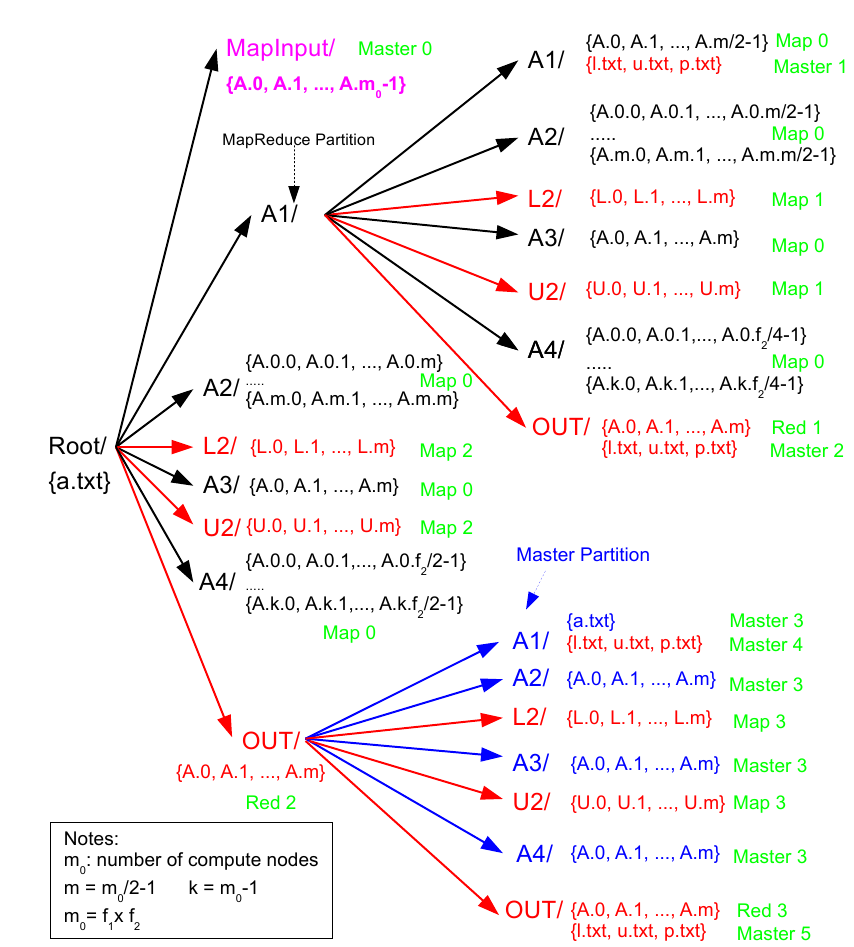
(adaptado de Xiang Jingen, 2013)
None.3 Descenso por el gradiente distribuido
Zinkevich et al., NIPS 2010
- Distribuir los datos al azar entre nodos
- Realizar descenso por el gradiente en cada nodo, por separado
- Unificar los resultados en un nodo central
Algoritmo en nodo worker

(adaptado de Zinkevich et al, 2010)
Algoritmo en nodo central

(adaptado de Zinkevich et al, 2010)