Aprendizaje Automático sobre
Grandes Volúmenes de Datos
Clase 2
Pablo Ariel Duboue, PhD
Universidad Nacional de Córdoba,
Facultad de Matemática, Astronomía y Física

None.1 Segunda Clase: Modelos
None.1.1 Features
Representando Instancias
-
Tipos de features
- booleanas (true, false)
- numéricas (4, 1, -5)
- de punto flotante o continuas (0.5, 1, 9.2)
- enumeraciones o discretas (rojo,azul,verde,amarillo)
Ejemplo: perros
- Si queremos representar un perro para una clasificación, depende del tipo de experimento
-
Para un experimento médico nos fijaremos en características físicas
- Tamaño (punto flotante)
- Peso (punto flotante)
- Edad en meses (numérico)
- Raza (enumeración)
-
Para un experimento de psicología canina nos fijaremos en características de comportamiento
- Agresivo (booleano)
- Edad en meses (numérico)
- Raza (enumeración)
- Cuidado con los datos superfluos
Representaciones diversas
-
Vamos a ver ahora ejemplos de como representar los siguientes tipos de datos:
- Texto
- Imágenes
- Árboles
- Trayectorias
- Tiempo
- Audio
- Algunas implementaciones están disponibles en http://scikit-learn.org/stable/modules/feature_extraction.html
Representando una palabra
-
Representando una sola palabra
- Enumeración
- Sufijos, prefijos
- Características particulares (todas mayúsculas, minúsculas)
- Idioma
Representando un texto
-
Bag of words
- Una feature por palabra, indicando si la palabra aparece en el texto o no (binaria) o cuantas veces aparece (numérico)
- Puede extenderse a pares de palabras (bigram model) o más
- Sólo se pueden usar palabras vistas durante el entrenamiento
-
word2vec: representaciones distribuidas
- Cada palabra se la representa como un vector de números de punto flotante de tamaño fijo
- Existe una relación geométrica entre las palabras y los contextos en los que aparecen (perro y gato están cercanas y así)
- http://code.google.com/p/word2vec/
Representando imágenes
- Campo de investigación muy activa
-
Método más sencillo: usar el valor de los píxeles directamente
- No generaliza muy bien
- Pero puede mejorar utilizando transformaciones algorítmicas del conjunto de entrenamiento
- Siguiente paso: tomar el promedio sobre pequeños cuadrados de la imágen
Representando imágenes
-
Métodos más complejos (SIFT/SURF)
- http://en.wikipedia.org/wiki/SURF

Representando árboles
-
Árboles pueden representarse como la secuencia de operaciones en un autómata a pila que lo reconozca
- Es la estructura de datos utilizada en un analizador sintáctico
- La secuencia en sí es un tipo de datos complejo, para transformarlo en features hay que trabajar más
-
Nodos en un árbol pueden representarse con el camino desde la raíz
- De vuelta, esta es una secuencia que es en sí un dato complejo
Representando trayectorias
-
Las trayectorias en general se representan
- Buscando vectores representativos
- Fijando el número de vectores que se utlizará para representar cada trayectoria
- En el caso más sencillo se utiliza un solo vector: del comienzo al fin de la trayectoria
Representando series en tiempo
- Series en el tiempo requieren algoritmos específicos
-
Pero pueden ser utilizadas con algoritmos genéricos tomando una ventana que se mueve en el tiempo y calculando información para cada ventana
- La información por cada ventana puede repetirse sobre un periodo de tiempo y entrenar sobre eso
- En general, los resultados son pobres
Representando audio
- Un caso particular de series en el tiempo es el audio
- La transformación de Fourier produce buenas features
- Procesamiento de voz utiliza aún más features como análisis de cepstrum y otras
Para feature engineering
-
En la clase de feature engineering vamos a ver otras técnicas:
- Binning: transformar una feature continua o numérica en una discreta (altura: 1.40m en altura: baja)
- Imputación: decidir qué valor se le asigna a features inexistentes
- Null flags: tener features que indican que una feature no existe
- Técnicas para lidiar con features dependientes estadísticamente hablando
None.1.2 Modelos
¿Qué es un modelo?
“Un ente que aprende que no asume nada acerca de la identidad del concepto objetivo no tiene ninguna base racional para clasificar cosas que nunca vio.”
Mitchel (1997)
- Los modelos capturan la información en los datos de entrada (o en los datos en general, en aprendizaje no supervisado)
- Representan la forma de ver el mundo que permite extrapolar cuando se observan nuevos datos (nunca vistos)
- Los modelos pueden ser matemáticamente bien formados (estadísticos) o simplemente algoritmicos (cascadas de if-then-else)
El modelo como código objeto
-
La clase pasada hablábamos de una metáfora de programación para el Aprendizaje Automático
- En dicha metáfora el modelo sería el código objeto obtenido a partir de los datos de entrenamiento
-
Diferenciamos el modelo del algoritmo usado para obtener el modelo
- De la misma manera que diferenciamos el código objeto del compilador que lo obtuvo
-
Muchos modelos tienen varios algoritmos que pueden ser usados para construirlos
- Entrenamiento de redes neuronales vía backpropagation vs. algoritmos genéticos
Propiedades de los modelos
- Sesgo inductivo
- El dilema del sesgo vs. varianza (bias–variance dilemma)
-
Para modelos estadísticos
- Modelos generativos
- Modelos discriminantes
- Teorema no-free lunch (NFL)
Sesgo inductivo
-
Distintos modelos asumen distintas cosas sobre la población de elementos a predecir
- Es importante entender este sesgo inductivo para comprender el comportamiento del modelo sobre una población dada
- http://en.wikipedia.org/wiki/Inductive_bias
-
Ejemplos de sesgo inductivo:
- Maximización de independencia condicional (Naïve Bayes)
- Minimización del error en cros-validación
- Maximización del borde (SVMs)
- Minimización del largo de la descripción
- Minimización del número de features
- Minimización de la distancia a casos conocidos
El conjunto de entrenamiento como modelo
-
Sistemas de Aprendizaje por Memorización (memory-based learning)
- Dada una función de distancia
- Asignar una clase dada la clase de elementos cercanos
- Algoritmo k-NN: k-nearest neighborgs
El dilema del sesgo vs. varianza
-
Un sistema que puede describir los datos de entrenamiento a la perfección (bajo sesgo estadístico) pero después ser malos a la hora de generalizar (presentar una varianza alta)
- http://en.wikipedia.org/wiki/Bias%E2%80%93variance_dilemma
- No hay una solución general (dado el NFL)
Ejemplo bias-variance dilemma
- Datos originales
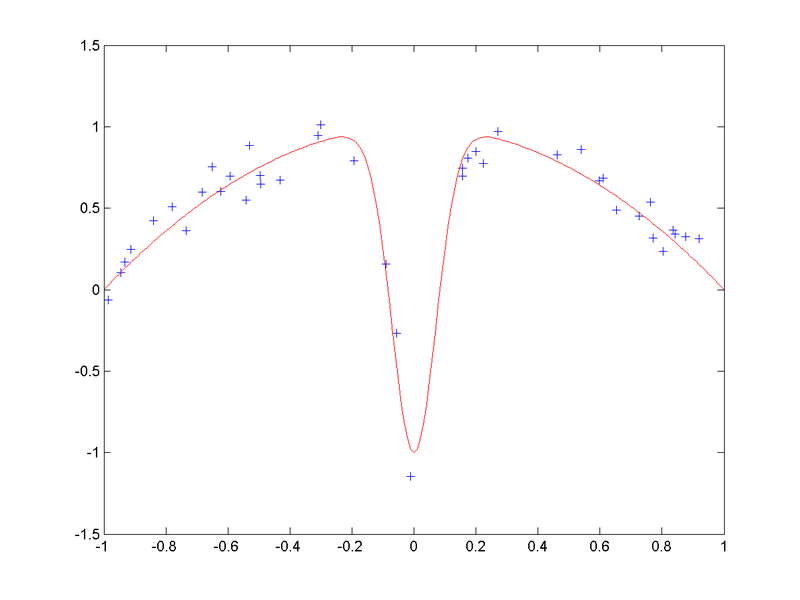
(CC-BY-SA Anders Sandberg)
Ejemplo bias-variance dilemma
- Aproximación RBF con alto sesgo estadístico
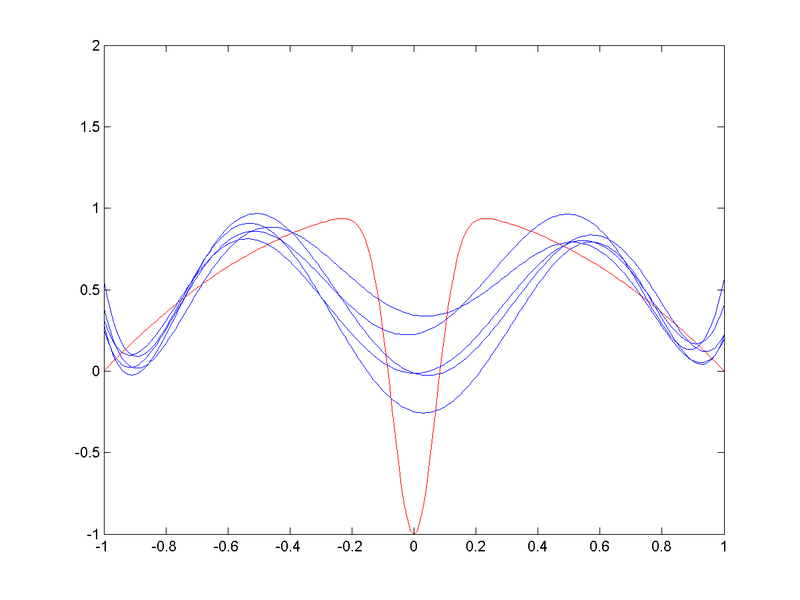
(CC-BY-SA Anders Sandberg)
Ejemplo bias-variance dilemma
- Relativamente buena aproximación RBF (pero con mayor varianza)
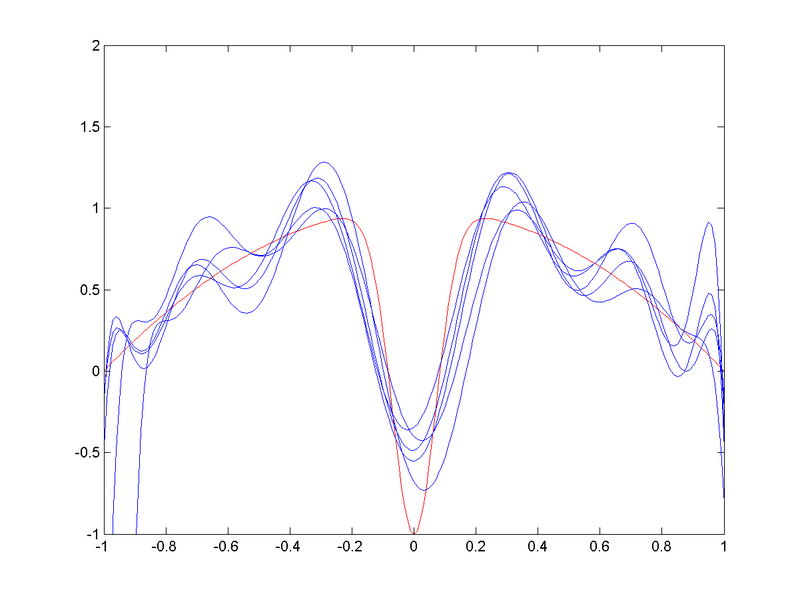
(CC-BY-SA Anders Sandberg)
Ejemplo bias-variance dilemma
- Aproximación RBF con bajo sesgo estadístico y alta varianza
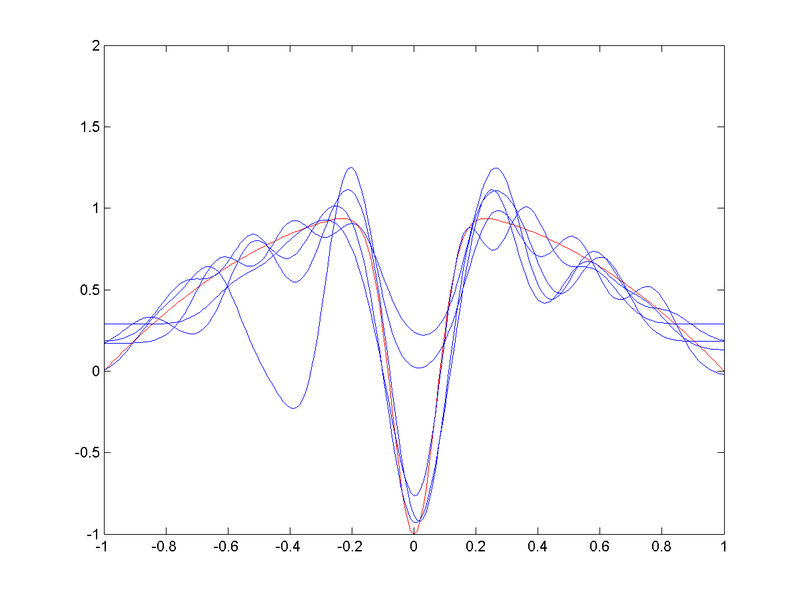
(CC-BY-SA Anders Sandberg)
Modelos Generativos vs. Discriminantes
-
Para modelos estadísticos
- Calcular la probablidad de la clase objetivo dada las features de entrada
- Podemos realizar este cálculo si tenemos un modelado probabilístico de la probabilidad conjunta de entradas y la clase objetivo
- Sin embargo, no es un requerimiento el modelado de la probabilidad conjunta
- Simulación vs. emulación
Modelos Generativos
- Calcular P(y|x1, …, xn) via P(x1, …, xn, y)
-
El cálculo de la probabilidad conjunta habilita sistemas reversibles
- Cualquier variable puede ser una clase objetivo
-
Requiere un “historia generativa” de como los datos existen y se interrelacionan
- Dependencia entre variables
-
Necesitan más datos y/o hacen uso menos eficiente de los mismos
- Si sólo nos interesa la clase objetivo, estamos modelando de más
Modelos Discriminantes
- Sólo se centran en modelar P(y|x1, …, xn)
-
Muchas veces ni siquiera modelan la probabilidad pero probabilidades sin normalizar
- Likelihoods
- Son suficientes para decidir entre distintos valores posibles de la clase objetivo
- Suelen ofrecer mejores resultados en la práctica
- Tienen menos ventajas teóricas
Teorema del No Free Lunch
- El teorema No Free Lunch dice que, dado una distribución de funciones objetivos que sea completamente al azar, no puede haber un algoritmo que funcione mejor sobre todas las funciones objetivo.
None.1.3 Evaluación
Evaluando modelos
- Medir cuantas veces un sistema devuelve la respuesta correcta (“exactitud/accuracy”) no es suficiente
-
Muchos problemas de interés práctico tienen un gran sesgo hacia una sola clase (clase de fondo)
- Si el 95% de las veces algo no ocurre, decir que nunca ocurrirá (¡un modelo que no es particularmente muy útil!) se equivocará sólo un 5% del tiempo
-
Datos apartados (no entrenar y testear sobre los mismos datos)
- Los datos apartados tienen que ser representativos del problema y la población donde se utilizará el sistema
-
Múltiples experimentos
- Cada vez que se ejecuta algo sobre los datos de evaluación, te cambian a uno mismo
Precision/Recall
- TP: true positives, los elementos anotados correctos
- FP: false positives, elementos anotados incorrectos
- FN: false negatives, elementos no anotados correctos
precision = (|correctamente anotado|)/(|anotado|) = (tp)/(tp + fp)
recall = (|correctamente anotado|)/(|habia que anotar|) = (tp)/(tp + fn)
Métrica F
- Promedio entre precision / recall
F = 2⋅(P⋅R)/(P + R)
- Puede incorporar un parámetro para darle más importancia a uno o el otro
Fβ = (1 + β²)⋅(P⋅R)/((β²⋅P) + R)
Ejemplo métrica F

ROC
- Cuando se puede variar Precision/Recall con un parámetro, esto forma una curva
- El área bajo esa curva nos dá la idea de que tan bien funciona un sistema
- Un sistema que funciona todo el tiempo con muy buena precision y recall, tendrá un área muy grande
- Un sistema que tiene gran precision pero clasifica pocas instancias y muy poca precision cuando clasifica muchas tendrá muy poca área
Promediado micro y macro
-
Cuando el sistema se ejecuta sobre varios conjuntos de testeo
- ¿Cómo definimos precision/recall?
-
Dos opciones:
- Acumulamos los TP/FP/FN sobre los distintos conjuntos: promediado micro (micro-averaging)
- Promediamos los resultados de precision/recall calculado en cada conjunto por separado: promediado macro (macro-averaging)
Trampas de evaluación
-
Errores comunes de evaluación
- Testear donde se entrenó
- Target leak: una de las features contiene la clase objetivo
-
En general, si algo no concuerda, no tiene sentido, hay que investigar
- Posible error de programación en el sistema de testeo
-
No quedarse sólo con los números, hacer análisis de errors viendo casos concretos
- Fácil detectar errores de código en el sistema
Concordancia entre anotadores
- “Inter-Coder Agreement for Computational Linguistics” por Artstein & Poesio (2008)
- http://aclweb.org/anthology/J/J08/J08-4004.pdf
-
“Assessing Agreement on Classification Tasks: The Kappa Statistic” por Carletta (1996)
- http://aclweb.org/anthology-new/J/J96/J96-2004.pdf
κ = (P(A) − P(E))/(1 − P(E))
donde P(A) es la concordancia observada yP(E) el la concordancia esperada por chance entre los anotadores si eligieran el mismo número de veces por cada categoría, al azar.
Ejemplo de la Kappa de Cohen
- De http://en.wikipedia.org/wiki/Cohen%27s_kappa
| B si | B no | |
| A si | 20 | 5 |
| A no | 10 | 15 |
- P(A) = (20 + 15)⁄50 = 0.7
- P(E) = P(E, yes) + P(E, no), A dice que si 50% y B dice que si 60%, por lo tantoP(E, yes) = 0.5 × 0.6 = 0.3 y P(E, no) = 0.5 × 0.4 = 0.2 y entoncesP(E) = 0.3 + 0.2 = 0.5
κ = (0.7 − 0.5)/(1 − 0.5) = 0.4
La computadora como otro anotador
- Cuando los anotadores no se ponen demasiado de acuerdo
- Agregar el resultado del sistema automático como otro anotador
- Si la evaluación entre anotadores se mantiene, entonces podemos concluir que la computadora se comporta de manera similar a los jueces humanos.
Ejemplo en biología
-
La clase anterior hablamos de un sistema que utilizaba datos anotados automáticamente
- Pero sólo en un 2.65% de los casos
- Este tipo de sesgo introducido en la recolección de datos podría invalidar el modelo
- Para evaluarlo, se utilizaron expertos en biología, pero su concordancia era baja (77% de a pares)
-
La computadora se comportaba como un juez humano más
- Y funcionaba mejor en el 2.65% de los casos que incluían la palabra clave (gen, proteína, mRNA) después de removerla
Métricas de evaluación ad-hoc
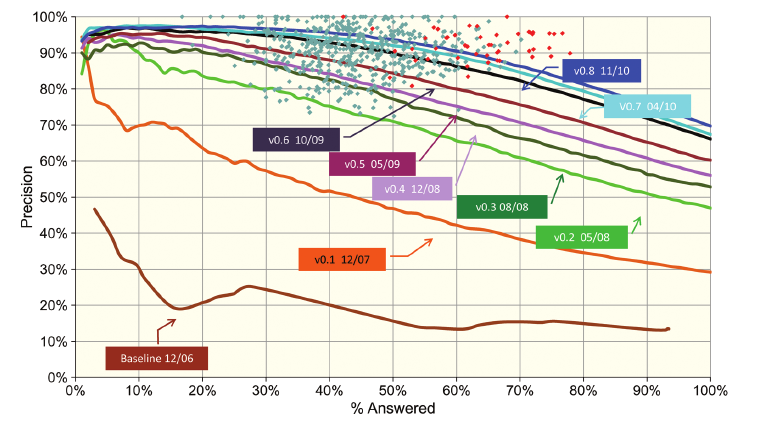
Overfitting
- Cuando el sesgo estadísitico disminuye demasiado y la varianza empieza a dispararse
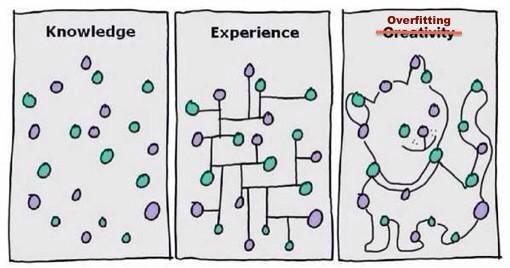
@AcademicSays
Overfitting
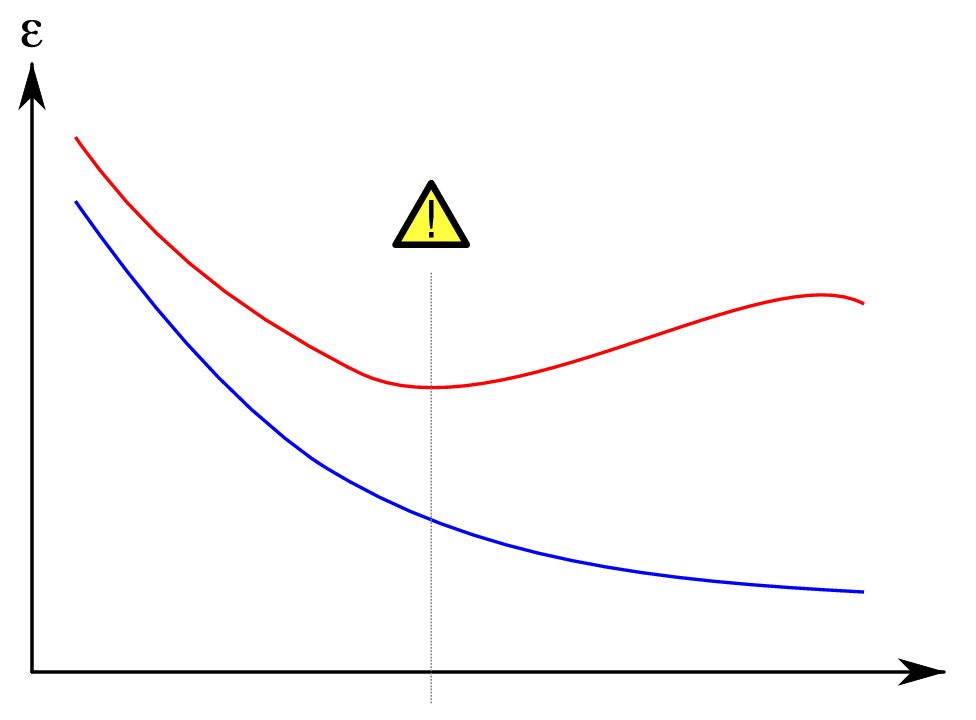
(CC-BY Gringer)
Aprendizaje interrumpido
- Para evitar el overfitting, podemos usar un conjunto extra para decidir cuando terminar de entrenar
- Esto se conoce como early termination
-
De cualquier forma no es la solución perfecta
- Teorema del No Free Lunch
Cros-validación
-
Prácticamente como entrenar y testear en los mismo datos
-
datos = {A,B,C}
- entrenar en A,B, testear en C
- entrenar en A,C, testear en B
- entrenar en B,C, testear en A
-
datos = {A,B,C}
-
Útil cuando se tienen pocos datos
- No debería ser nuestro caso
¿Cuántos datos? Curvas de aprendizaje
- Para tener una idea de si el sistema está aprendiendo con los datos disponibles
-
Tomar una muestra al azar más pequeña
- Evaluar en un porcentaje de la misma
- O hacer cros-validación
- Hacer una curva a medida que el tamaño de la muestra aumenta
- Si el muestreo se repite varias veces para cada tamaño, es posible graficar también la varianza
Ejemplo de curva de aprendizaje
Filtering Personal Queries from Mixed-Use Query Logs por A. Bressane Neto, P. Desaulniers, P.A. Duboue, A. Smirnov (Canadian AI, 2014)
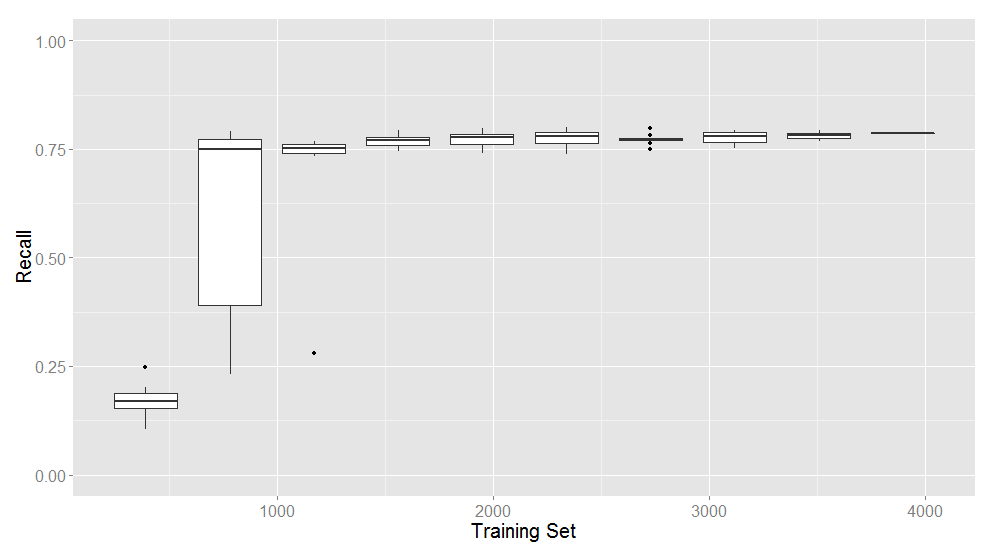
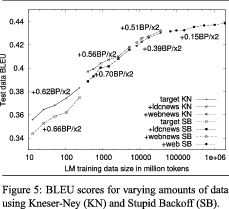
Curva de aprendizaje sobre grandes volúmenes de datos
Large Language Models in Machine Translation por T. Brants, A.C. Popat, P. Xu, F.J. Och, J. Dean (EMNLP-CoNLL, 2007)