Aprendizaje Automático sobre
Grandes Volúmenes de Datos

Clase 3

Pablo Ariel Duboue, PhD

Universidad Nacional de Córdoba,
Facultad de Matemática, Astronomía y Física

None.1 Tercera Clase: Clasificación

None.1.1 Preguntas de la clase anterior

Material de lectura

Clase pasada:
- Capítulo 2 del Mitchel (1997)
- Wolpert, D.H., Macready, W.G. (1997), "No Free Lunch Theorems for Optimization," IEEE Transactions on Evolutionary Computation 1, 67
- http://en.wikipedia.org/wiki/Inductive_bias
- http://en.wikipedia.org/wiki/Overfitting
- http://en.wikipedia.org/wiki/SURF
Ésta clase:
- Capítulos 3 y 6 del Mitchel (1997)
- Gale, William A. (1995). "Good–Turing smoothing without tears". Journal of Quantitative Linguistics 2: 3. doi:10.1080/09296179508590051

Utilización de representaciones vectoriales

Para un ejemplo de uso, véase: https://github.com/radialpoint/word2vec-query-expansion
./word2vec -train text8 -output sample.vectors.txt -cbow 0 -size 5 -window 5 -negative 0 -hs 1 -sample 1e-3 -threads 12 -binary 0
dog 0.4310, 0.2284, 0.2320, -0.0833, -0.2817

cat 0.4779, 0.1520, 0.1939, -0.0522, -0.3998

abandoned -0.1811, -0.3267, 0.3308, -0.6027, 0.3290
En 160 mil documentos palabras más parecidas a dog: puppy 0.732681 poodle 0.654978 puppies 0.638696 barking 0.627683 doggie 0.625534

Representación de árboles vía árbol común

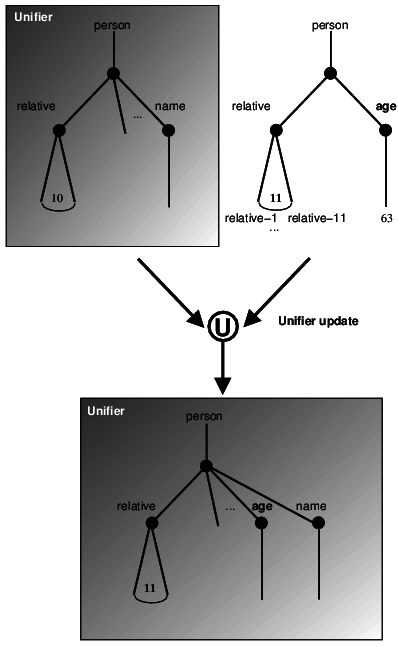
None.1.2 Naive Bayes

Teorema de Bayes

La probabilidad de dos eventos es igual a la probabilidad de un evento por la probabilidad del otro dado el primero:

P(A|B)P(B) = P(B|A)P(A) = P(A, B)

Despejando para una sola probabilidad condicional:

P(A|B) = (P(B|A)P(A))/(P(B))

En aprendizaje

Los eventos que nos interesan son la clase objetivo y las features

P(y|f⃗) = (P(f⃗|y)P(y))/(P(f⃗))

Dos lecturas

Estimador MAP: maximum a posteriori
- y_MAP = max_yP(f⃗|y)P(y)
Estimador ML: maximum likelihood
- y_MAP = max_yP(f⃗|y)

Teorema de Bayes: Ejemplo

Adaptado de Mitchel(1997)
- P(cancer) = 0.008, P(¬cancer) = .992
- P(⊕|cancer) = .98, P(⊖|cancer) = .02
- P(⊕|¬cancer) = .03, P(⊖|¬cancer) = .97
MAP:
- P(cancer|⊕) = P(⊕|cancer)P(cancer) = (.98).008 = .0078
- P(¬cancer|⊕) = P(⊕|¬cancer)P(¬cancer) = (.03).992 = .0298
- MAP es ¬cancer
  - Importancia de los priors

Naive Bayes

Naive Bayes asume que las features son probabilisticamente independientes
- y_NB = max_yP(f₁, ..., f_n|y)P(y) = max_yP(f₁|y)...P(f_n|y)P(y)
Podemos estimar P(f_i|y) a partir de conteos
Realizar el cálculo en espacio logarítmico para evitar underflow

Ejemplo

URL Classy: https://github.com/DrDub/urlclassy
http://drdub.github.io/urlclassy/example/
- Predecir qué tipo de URL es un link según el texto del URL
- http://www.autoparts.com/
  - Shopping: 1.5576913975184621e-27
  - Regional: 1.1477700187850885e-30
  - Business: 1.7084999074448435e-32
Features: secuencias de 4 letras ({www., ww.a, w.au, .aut, auto, utop, topa, opar, part, arts, rts., ts.c, s.co, .com})
Clase objetivo: 15 categorías

Ejemplo: datos

dmoz.org: Open Directory Project
Main Category Sub Category URL
- Arts Animation http://shotani.www2.50megs.com/animen_uno.html
- Arts Animation http://valleyofazure.tripod.com/
- Arts Animation http://www.angelfire.com/anime2/bestanimecharacters/
- Arts Animation http://www.angelfire.com/anime2/ninisbishonen/
- Arts Animation http://www.angelfire.com/grrl/magicshoppe2/
- Arts Animation http://www.angelfire.com/nv/neko/
- Arts Animation http://anime-alberta.org/
- Arts Animation http://animeclub.org/
4,137,187 rows, 548 subcategories, 15 top level categories

Ejemplo: conteos

Categoría Arte
- "ime.": 37
- "bert": 155
Categoría Negocios
- "ime.": 15
- "bert": 50

Estimando datos ausentes: smoothing

Estimar probabilidades a partir de conteos tiene el problema de que muchos datos no son observados
- ¿Qué hacer si un feature nunca aparece con un valor particular de la clase objetivo?
- Técnicas de smoothing: quitar masa de probabilidad de los eventos observados para dársela a los eventos no observados
- Sin smoothing la multiplicación de Naive Bayes da cero en muchos casos
Opciones sencillas:
- Lagrangiano: todo evento no observado se considera ocurre una vez
- ELE:agregar 0.5 a todos los conteos
- Add-tiny: agregar un número muy pequeño a todos los conteos

None.1.3 Árboles de decisión

Idea

Dividir los datos según un feature solo y un predicado simple sobre ese feature

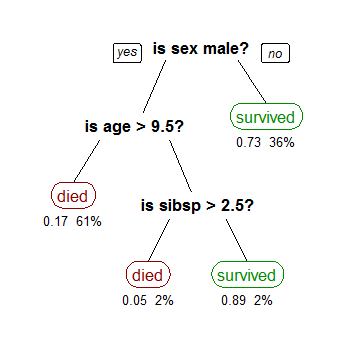
(CC-BY-SA Stephen Milborrow, from Wikipedia)

Impuridad de Gini

Una medida de qué tan bien se parte el conjunto de datos utilizando un feature en particular
- Qué tan bien sería categorizado un elemento al azar si se recategorizaran todos los elementos usando la distribución de probablidad inducida por sus categorías
- I_G(f) = ∑^m_i = 1f_i(1 − f_i) = ∑^m_i = 1(f_i − f_i²) = ∑^m_i = 1f_i − ∑^m_i = 1f_i² = 1 − ∑^m_i = 1f_i²
  - donde hay m categorías y en una partición hay f_i elementos en cada categoría
En el aprendizaje de árboles CART, se elige una partición que minimize la impuridad de Gini

Information Gain

Sinónimo de la Kullback-Leibler divergence, una de las funciones más útiles para aprendizaje automático
- Dice qué tan bien se puede explicar una nueva distribución de probabilidad si sabemos una dada
- Genera una medida no simétrica de la distancia entre dos distribuciones
D_KL(P∥Q) = ∑_iln⎛⎝(P(i))/(Q(i))⎞⎠P(i).
Usando la nomenclatura de la impuridad de Gini:
- I_E(f) = − ∑^m_i = 1f_ilog₂f_i
ID3, C4.5 tratan de maximizar la ganancia de información en cada split

ID3

ID3 (Ejemplos, Clase Objetivo, Features)

Crear un nodo raíz

Si todos los ejemplos son positivos, devolver la raíz con clase +

Si todos los ejemplos son negativos, devolver la raíz con clase -

Si no quedan features, devolver la raíz con clase igual al valor más común

Caso contrario

A ← la feature que mejor clasifica los ejemplos
El feature en la raíz es A
Para cada valor posible v_i del feature A

Agregar rama al árbol bajo la raíz (testeo A=v_i)
Sean Ejemplos(v_i) el subconjunto de los ejemplos que tienen v_i para A
Si Ejemplos(v_i) está vacío, para esta rama setear la clase al valor objetivo más común
Sino agregar un subárbol ID3 (Ejemplos(v_i), Clase Objetivo, Features– {A})

Devolver la raíz