Aprendizaje Automático sobre
Grandes Volúmenes de Datos
Clase 4
Pablo Ariel Duboue, PhD
Universidad Nacional de Córdoba,
Facultad de Matemática, Astronomía y Física

None.1 Cuarta Clase: Clasificación
None.1.1 Preguntas de la clase anterior
Material de lectura
-
Clase pasada:
- Capítulos 3 y 6 del Mitchel (1997)
-
Ésta clase:
- Gale, William A. (1995). "Good–Turing smoothing without tears". Journal of Quantitative Linguistics 2: 3. doi:10.1080/09296179508590051
- Capítulo 5 del Marlsand (2009) "Machine Learning, an Algorithmic Perspective"
- Capítulo 5 del Smola & Vishwanathan (2008) "Introduction to Machine Learning"
- http://en.wikipedia.org/wiki/Logistic_regression
- http://en.wikipedia.org/wiki/Linear_regression
Preguntas
-
Cantidad de datos negativos?
- Estimación de priors, muchas veces por fuera del aprendizaje automático en sí (análisis de datos)
- Pipeline de trabajo para clasificación: próxima clase
- Random forests: vamos a tener una clase dedicada a ellos en la segunda parte de la materia
Comentarios del feedback
- Palabras finales sobre word2vec: ejemplo de features interesantes, pero no es parte de la clase
- Aplicaciones específicas: fuera del alcance de la materia
- Feedback es obligatorio y firmado, incluyan si son alumnos de grado, posgrado u oyentes
- Material más introductorio: algunos alumnos están cursando MOOCs de aprendizaje automático, si pueden compartir sus experiencias en la lista de correo
NB: de conteos a probabilidades
- Conteos de instancias (Ni) vs. conteos de features (Nf)
-
De la definición de probabilidad conjunta:P(".com"|Arts)P(Arts) = P(".com", Arts) = (Nf(".com", Arts))/(Nf(.))
-
De la definición de probabilidad simple:P(Arts) = (Ni(Arts))/(Ni(.))
-
Despejando para la probabilidad condicional:P(".com"|Arts) = (Ni(.))/(Nf(.))(Nf(".com", Arts))/(Ni(Arts))
Ejemplo de NB
1
$git clone https://github.com/DrDub/urlclassy.git
$ node
> eval(fs.readFileSync("example/features.js").toString()); eval(fs.readFileSync("example/classifier.js").toString())
> trained_classifier.totalExamples
373260
> trained_classifier.classTotals.Arts
18732
> trained_classifier.classTotals.Business
18477
NB: Conteos
Arte:
Negocios:
| \strikeout off\uuline off\uwave offwww. | 13957 |
| \strikeout off\uuline off\uwave offww.a | 1967 |
| \strikeout off\uuline off\uwave offw.au | 56 |
| \strikeout off\uuline off\uwave off.aut | 11 |
| \strikeout off\uuline off\uwave offauto | 6 |
| \strikeout off\uuline off\uwave offutop | 3 |
| \strikeout off\uuline off\uwave offtopa | 2 |
| \strikeout off\uuline off\uwave offopar | 9 |
| \strikeout off\uuline off\uwave offpart | 42 |
| \strikeout off\uuline off\uwave offarts | 150 |
| \strikeout off\uuline off\uwave offrts. | 70 |
| \strikeout off\uuline off\uwave offts.c | 128 |
| \strikeout off\uuline off\uwave offs.co | 2567 |
| \strikeout off\uuline off\uwave off.com | 13203 |
| \strikeout off\uuline off\uwave offwww. | 17115 |
| \strikeout off\uuline off\uwave offww.a | 1517 |
| \strikeout off\uuline off\uwave offw.au | 64 |
| \strikeout off\uuline off\uwave off.aut | 24 |
| \strikeout off\uuline off\uwave offauto | 49 |
| \strikeout off\uuline off\uwave offutop | 2 |
| \strikeout off\uuline off\uwave offtopa | 2 |
| \strikeout off\uuline off\uwave offopar | 5 |
| \strikeout off\uuline off\uwave offpart | 73 |
| \strikeout off\uuline off\uwave offarts | 48 |
| \strikeout off\uuline off\uwave offrts. | 84 |
| \strikeout off\uuline off\uwave offts.c | 392 |
| \strikeout off\uuline off\uwave offs.co | 3581 |
| \strikeout off\uuline off\uwave off.com | 14495 |
Ejemplo de NB
2
> var p_arts = trained_classifier.classTotals.Arts / trained_classifier.totalExamples; p_arts
0.0501848577399132
> var p_business = trained_classifier.classTotals.Business / trained_classifier.totalExamples; p_business
0.04950168783153834
> var ml_arts=1.0; for(var i=0; i<w.length;i++){var y=trained_classifier.classFeatures.Arts[trained_features[w[i]]]; if(y){ml_arts*=y / trained_classifier.classTotals.Arts}}; ml_arts
1.6008344829669292e-32
> var ml_business=1.0; for(var i=0; i<w.length;i++){var y=trained_classifier.classFeatures.Business[trained_features[w[i]]]; if(y){ml_business*=y/ trained_classifier.classTotals.Business}}; ml_business
4.330609317975143e-31
None.1.2 Smoothing
Estimando datos ausentes: smoothing
-
Estimar probabilidades a partir de conteos tiene el problema de que muchos datos no son observados
- ¿Qué hacer si un feature nunca aparece con un valor particular de la clase objetivo?
- Técnicas de smoothing: quitar masa de probabilidad de los eventos observados para dársela a los eventos no observados
- Sin smoothing la multiplicación de Naive Bayes da cero en muchos casos
-
Opciones sencillas:
- Lagrangiano: todo evento no observado se considera ocurre una vez
- ELE:agregar 0.5 a todos los conteos
- Add-tiny: agregar un número muy pequeño a todos los conteos
Simple Good-Turing
| Frecuencia | Frecuencia de la frecuencia |
| r | Nr |
| 1 | 120 |
| 2 | 40 |
| 3 | 24 |
| 4 | 13 |
| 5 | 15 |
| 6 | 5 |
| 7 | 11 |
| 8 | 2 |
| 9 | 2 |
| 10 | 1 |
| 11 | 0 |
| 12 | 3 |
Estimador r*
- Si N = ∑rNr, queremos estimar la probabilidad pr para los objetos que vimos r veces:
pr ≡ (r*)/(N)
- Un estimador MLE será pr = r⁄N (o sea r* = r) y predice la probabilidad de los elementos ausentes como cero (no es muy útil)
- El estimador Good-Turing utiliza:
r* = (r + 1)(E(Nr + 1))/(E(Nr))
-
Good-Turing estima la probabilidad ausente como N1⁄N
- N1es la frecuencia de frecuencias mejor medida por lo que E(N1) = N1es una buena aproximación
Distribución de Zipf
Frecuencia de palabras en Wikipedia:
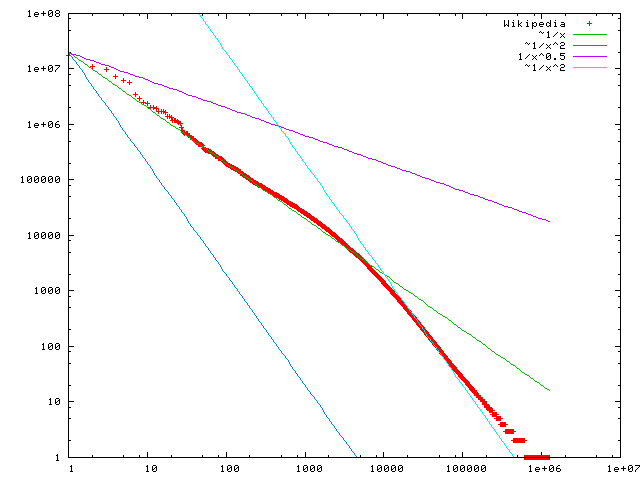
(LGPL por Victor Grishchenko)
Usándolo en la práctica
- Ajustar la probabilidad de los eventos observados usando los nuevos estimadores
-
Distribuir la masa de probabilidad para los eventos no observados (N1⁄N) a medida que aparecen
- ¿Pero cuántos hay?
- ¿Cómo distribuir esta probabilidad entre ellos?
-
Si es posible, se usa conocimiento extra sobre la estructura de los eventos
- Por ejemplo, si los eventos son pares de palabras, podemos estimar qué tan importante es un par que nunca vimos en función de cuán frecuentes son las palabras que lo componen
None.1.3 SVMs
Separador de gran márgen
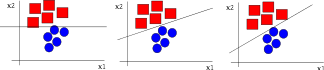
Un separador de gran márgen: mayor expectativa de mejor generalización
Intución
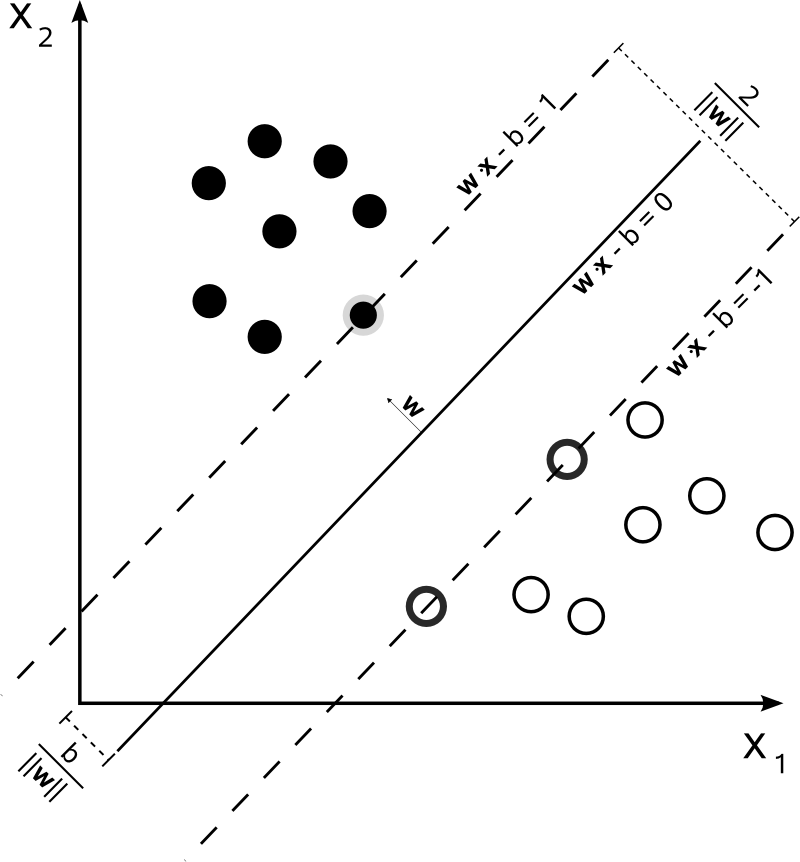
-
Optimizar w⋅x − b = 0 se puede resolver vía optimización de programación cuadrática
- Si no existe hiperplano de separación, proyectamos a más dimensiones donde es más fácil que exista
Separación en altas dimensiones
-
Pasar de las features originales a features extendidas
- Incrementar la dimensionalidad
- Por ejemplo, pasar de dos dimensiones x1, x2a seis dimensiones 1, √(2)x1, √(2)x2, x1x2, x21, x22
- La función de expansión se llama kernel
Kernel Trick
- Hacer una optimización de programación cuadrática en gran cantidad de dimensiones sería muy costoso
- Pero en la optimización, si la función de expansión (kernel) tiene buenas propiedades es posible evitar la gran dimensionalidad y realizar todas las operaciones en la dimensión original
- SVMs son conceptualmente sencillas, la complejidad radica en lograr que esas ideas sencillas sean factibles de computar
None.1.4 Regresión Logística
Regresión Lineal
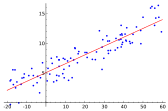
yi = β1xi1 + ⋯ + βpxip + εi = x\rmTiβ + εi, i = 1, …, n
Estimación por least-squares
Representando en forma matricial y = Xβ + ε donde
y =
y1
y2
⋮
yn
, X =
x\rmT1
x\rmT2
⋮
x\rmTn
=
x11
⋯
x1p
x21
⋯
x2p
⋮
⋱
⋮
xn1
⋯
xnp
, β =
β1
β2
⋮
βp
, ε =
ε1
ε2
⋮
εn
entonces podemos hacer una solución cerrada para β:
β̂ = (X\rmTX) − 1 X\rmTy = ( ∑xix\rmTi ) − 1( ∑ xiyi )
Función Logística
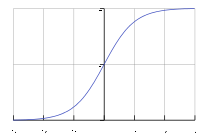
F(t) = (et)/(et + 1) = (1)/(1 + e − t)
Regresión Logística: intuición
- Pasar del espacio de la función objetivo al espacio de probabilidad de que la función objetivo sea de una clase determinada
- Minimizar el error de una combinación lineal de features después de aplicar la función logística para obtener una probabilidad
- No tiene solución cerrada, se utilizan métodos de tipo Newton para encontrar una solución aproximada
Distribuciones de la familia exponencial
-
Una de las más versátiles
- Incluyen Gaussianas, Poisson, Gamma, etc
- Llevan a problemas de optimización convexos (solubles computacionalmente)
- Describen la distribución de probabilidad como modelos lineales