Aprendizaje Automático sobre
Grandes Volúmenes de Datos
Clase 6
Pablo Ariel Duboue, PhD
Universidad Nacional de Córdoba,
Facultad de Matemática, Astronomía y Física

None.1 Sexta Clase: Aprendizaje No Supervisado
None.1.1 Clase anterior
Material de lectura
-
Clase pasada:
- Capítulo 13 del Owen et al. (2012)
- http://ufal.mff.cuni.cz/~zabokrtsky/courses/npfl104/html/feature_engineering.pdf
-
Ésta clase:
- Jacob Kogan: Introduction to Clustering Large and High-Dimensional Data (2007)
-
Wikipedia: Cluster Analysis (Evaluation of clustering results)
- http://en.wikipedia.org/wiki/Cluster_analysis#Evaluation_of_clustering_results
- Halkidi, Batistakis & Vazirgiannis: On Clustering Validation Techniques. Journal of Intelligent Information Systems December (2001), Volume 17, Issue 2-3, pp 107-145.
- Everitt, Landau & Leese: Cluster Analysis (2001)
- Capítulo 7 del Owen et al. (2012)
Preguntas
- Binning: una técnica de reducción del espacio de valores (de 256 valores de una byte a 3 valores)
- Feature selection: ¿cuántas features? No se sabe bien, tomar un porcentaje de las mejores es una posibilidad
-
Clustering e ingeniería de features:
- una técnica de binning muy usada es particionar los datos y usar el cluster en vez del dato original
- Técnicas de clustering se usan mucho con lenguaje natural, para tener features más informativas que simplemente palabras
- Pre-procesamiento no-supervisado de las features de entrada es la clave de Deep Learning
Reducción de dimensionalidad
-
Selección de features es una técnica de reducción de dimensionalidad
- Otras involucran todas las features a la vez y generan un cambio de coordenadas, de un espacio mayo a uno menor
- Una muy utilizada es descomposición en valores singulares (SVD) o también llamada análisis de componentes principales (PCA)
- Tomamos nuestras instancias como filas y armamos una matriz M, entonces
MTME = EL
- donde E es la matriz de los autovectores y L es la matriz diagonal de los autovectores
- Si Ek son las primeras k columnas de E, entonces MEk es una representación en k dimensiones de M
- Véase http://infolab.stanford.edu/~ullman/mmds/ch11.pdf
En qué van a ser evaluados
-
Dos algoritmos en detalle:
- Naive Bayes
- Decision Trees
-
Dos algoritmos a nivel conceptual:
- SVM
- Regresión logística
- Ingeniería de features a nivel conceptual (práctico va a ser en la competencia kaggle y/o el proyecto)
Recordatorio
-
El sitio Web de la materia es http://aprendizajengrande.net
- Allí está el material del curso (filminas, audio)
-
Leer la cuenta de Twitter https://twitter.com/aprendengrande es obligatorio antes de venir a clase
- Allí encontrarán anuncios como cambios de aula, etc
- No necesitan tener cuenta de Twitter para ver los anuncios, simplemente visiten la página
-
Suscribirse a la lista de mail en aprendizajengrande@librelist.com es optativo
- Si están suscriptos a la lista no necesitan ver Twitter
-
Feedback es obligatorio y firmado, incluyan si son alumnos de grado, posgrado u oyentes
- El "resúmen" de la clase puede ser tan sencillo como un listado del título de los temas tratados
None.1.2 Aprendizaje No Supervisado
Aprendiendo lo que uno no sabe
- Un poco mágico
- Tenemos un modelo, queremos estimar sus parámetros
- Tenemos parámetros, queremos construir un modelo
- Conocer la respuesta, buscar la pregunta
- Muy ligado al concepto de distancia entre instancias
Mi tesis
- Mi tesis doctoral (http://duboue.net/thesis.html) consistió en una mezcla de aprendizaje supervisado y no supervisado
- Datos: texto e información simbólica sin alinear
cc
5cm\smallActor, bornThomasConneryonAugust25, 1930, inFountainbridge, Edinburgh, Scotland, thesonofatruckdriverandcharwoman.Hehasabrother, Neil, bornin1938.ConnerydroppedoutofschoolatagefifteentojointheBritishNavy.Conneryisbestknownforhisportrayalofthesuave, sophisticatedBritishspy, JamesBond, inthe1960s.…
amp;
5cm\includegraphics[width = 5cm]graph
None.1.3 Clustering
Clustering
- Un tipo de aprendizaje no supervisado
- Descubre estructura presente en los datos
-
Knowledge Discovery and Data Mining
- El objetivo de los métodos de clustering es descubrir grupos significativos presentes en los datos
- ¿Cómo evaluar algo que no sabíamos que existía?
Una cuestión de distancias
- El concepto central en clustering es la definición de una distancia entre instancias
- Cada definición de distancias induce un agrupamiento de los datos, basado en esa métrica
-
La distancia es donde se incorpora la información humana
- Entre otros puntos, por ejemplo, el número de clusters
Ejemplos de distancias
-
Datos de censo de la clase anterior:
- age: continuous.
- workclass: Private, Self-emp-not-inc, Self-emp-inc, Federal-gov, Local-gov, State-gov, Without-pay, Never-worked.
- sex: male, female.
- education: Bachelors, Some-college, 11th, HS-grad, Prof-school, Assoc-acdm, Assoc-voc, 9th, 7th-8th, 12th, Masters, 1st-4th, 10th, Doctorate, 5th-6th, Preschool.
- education-num: continuous.
- marital-status: Married-civ-spouse, Divorced, Never-married, Separated, Widowed, Married-spouse-absent, Married-AF-spouse.
- occupation: Tech-support, Craft-repair, Other-service, Sales, Exec-managerial, Prof-specialty, Handlers-cleaners, Machine-op-inspct, Adm-clerical, Farming-fishing, Transport-moving, Priv-house-serv, Protective-serv, Armed-Forces.
Ejemplo de distancia
- Un polinomio con coeficientes ad hoc y distancias ad hoc para cada componente
dist(i1, i2) = α1distage(age1, age2) + α2distworkclass(workclass1, workclass2) + α3disteducation(education1, education2) + …
-
Donde las distancias por componente pueden ser definidas matemáticamente o vía una tabla:
- distage(x, y) = (x − y)2
-
distworkclass(a, b) =
a/b private self gov’t unpaid private 0 0.3 0.7 1.0 self 0 0.9 0.7 gov’t 0 0.3 unpaid 0
Tipos de clustering
- Algoritmos por partición
- Algoritmos jerárquicos
- Algoritmos por densidad
- Algoritmos "fuzzy"
Algoritmos por partición
- Partir los datos en un número de particiones (clusters) donde no hay relaciones fuera de las particiones
-
Las particiones optimizan una cierta función objetivo
- La función objetivo enfatiza estructura local o global de los datos y su optimización es usualmente un proceso iterativo
- El número de clusters es normalmente un parámetro del algoritmo
- El más conocido es K-Means que vamos a ver hoy
- Otros ejemplos incluyen PAM y CLARA
Algoritmos jerárquicos
- Van uniendo clusters más pequeños en clusters más grandes o dividiendo clusters más grandes
-
El resultado es un árbol de clusters (un dendrograma)
- Puede ser transformado en una partición cortando el dendrograma a un nivel particular
- Aglomerativo
- Divisivo
- El algoritmo más sencillo requiere una matrix de proximidad completa
- Un algoritmo más eficiente es BIRCH (incremental, bueno con datos con ruido pero sensible al órden y limitado en tamaño)
Todos los pares
- Calcular la matrix de proximidad de manera completa es intratable para gran número de datos
-
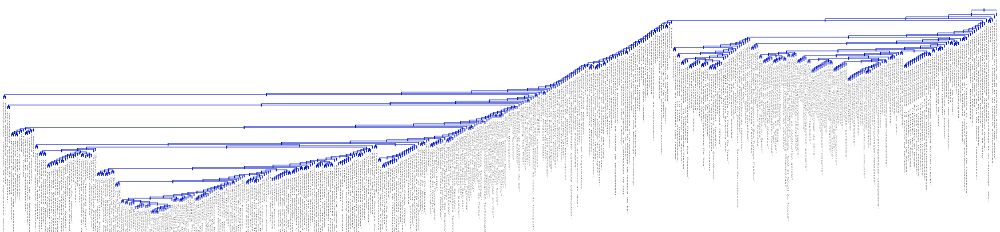
Ejemplo de dendrograma
- Cargos laborales, distancia es la proximidad de los textos de sus perfiles en LinkedIn
- Trabajo realizado para MatchFWD (Montreal, 2011)
Algoritmos por densidad
- Los clusters se consideran regiones del espacio de datos de alta densidad, separados por regiones de baja densidad.
-
El más conocido es DBSCAN
- La idea detrás de DBSCAN es que para cada punto en el cluster, un entorno de cierto radio debe contener un mínimo número de puntos en el cluster.
- Soporta ruido (outliers) y puede descubrir clusters de forma arbitraria.
- Tiene parámetros complejos de elegir, como el radio y el número de puntos en el entorno
Algoritmos "fuzzy"
- En estos algoritmos, un punto pertenece a más de un cluster
- La membresía no es “exacta”, pero un número real entre 0 y 1.
-
Los más conocidos son variantes probabilística de K-Means, que se basan en una mezcla de distribuciones Gaussianas (entrenadas usando el algoritmo EM).
- Los centros de los clusters son la media de las distribuciones Gaussianas
- Se estima la probabilidad de que cada punto sea generado por la Gaussiana número j (que pertenezca al cluster j)
- La asignación de puntos a clusters asume que los puntos están generados por una distribución normal
- La estimación se hace con el algoritmo de Expectación Maximización (EM)
K-Means
-
Se basa en el concepto de elementos sintéticos:
- cada cluster se lo representa por un centroide, un elemento ficticio
- en vez de calcular la distancia a todos los elementos del cluster, se la calcula sólo al elemento ficticio
- El algoritmo recibe como parámetro el número K de clusters
- Al comienzo se toman como centroides K elementos al azar
- En cada paso, se re-clasifican los elementos según el centroide al que están más cerca
-
Para cada cluster, se re-calcula el centroide como la media de los elementos del cluster
- ¿Cómo calcular el centroide? Depende de los datos, igual que la distancia.
K-Means, gráficamente
- Primero y segundo paso. Los elementos línea punteado son los centroides.
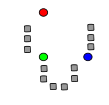
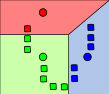
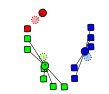
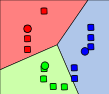
(Wikipedia)
Un cluster dominante
- Muchas veces K-Means produce un sólo cluster dominante
- En ese caso es posible volver a ejecutar K-Means en ese cluster y obtener un tipo de clustering jerárquico
- Lo más probable es que la función de distancia es pobre y no permite distinguir bien entre los elementos originales
MatchFWD: Problem
Ejemplo de Clustering
- Queremos agrupar empresas en función de que tan similares son sus culturas corporativas
- Distancia: qué tan similares son dos empresas basado en la gente que trabajo en ambas:
distancia(compañía1, compañía2) = (|gente trabajó para ambas|)/(|gente trabajó para cualquiera|)
¿Cuántos clusters?
-
Canopy Cluster
- Una técnica de fuzzy clustering
- Realizar el clustering con distintos valores de K y elegir el valor que produce mejores resultados de evaluación
-
Métricas específicas
- Ver Halkidi et al (2001)
Etapas del proceso de Clustering
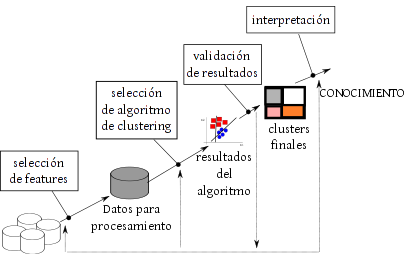
Adaptado de Halkidi et al (2001), Fig. 1
Validando Clusters
-
Tipos de validación
-
Validación vs. Evaluación
- Porque estamos viendo cosas que no sabíamos antes
- Interna: qué tan “compactos” y “robustos” son nuestros clusters
- Externa: qué tan bien se ven comparados con clusters objetivo
- Contra la hipótesis null: qué tan bien se ven comparados con clusters al azar
-
Validación vs. Evaluación
Validación Interna
- Coeficiente de silueta
- Índice de David-Bouldin
- Índice de Dunn
- Correlación Cofenética (para dendagramas)
- Partición de muestras (para robustez)
Métricas de Berry y Linoff
-
Compactitud, los miembros de cada cluster deben estar tan cercanos entre ellos como sea posible.
Metric: variance (to minimize). -
Separación, los cluster deben estar muy espaciados entre sí.
Medimos la distancia entre los dos clusters:Linkeo simple mide la distancia entre los miembros de los clusters.Linkeo compleo mide la distancia entre los miembros más distantes.Comparación de centroides mide la distancia entre los centros de los clusters.
Coeficiente de Silueta
-
El coeficiente de silueta asocia un escalar s(x⃗) del dataset. Si ∏ = {π1, …, πk} es el clustering, entonces:
- Computer I(x⃗) = (1)/(|πi|)∑x’⃗ ∈ πid(x⃗, x⃗’), la distancia promedio de x⃗ a todos los otros puntos en el mismo cluster
- Para j ≠ i, calcular Oj(x⃗) = (1)/(|πj|)∑x’⃗ ∈ πjd(x⃗, x⃗’), la distancia promedio de x⃗ a los otros puntos en clusters diferentes y O(x) = min{O1(x⃗), …, Oi − 1(x⃗), Oi + 1(x⃗), …, ⃗Ok(x⃗)} (se omite \strikeout off\uuline off\uwave offOi(x⃗)\uuline default\uwave default)
- El coeficiente de silueta entonces es
s(x⃗) = (O(x⃗) − I(x⃗))/(max{O(x⃗), I(x⃗)}) - − 1 < s(x⃗) < 1
- s(x⃗) < 0 ⇒ x⃗ estaría mejor en otros clusters
- s(x⃗) ≈ 1 ⇒ πi es “denso”
- El coeficiente para un cluster o una partición es el promedio de los s(x⃗) en el cluster o la partición
Índice de David-Bouldin
DB = (1)/(n)n⎲⎳i = 1maxi ≠ j⎛⎝(σi + σj)/(d(ci, cj))⎞⎠
donde
- n es el número de clusters
- cx es el centroide del cluster x
- σx es la distancia promedio de todos los elementos del cluster x
- d(ci, cj) es la distancia entre centroides ci y cj
-
DB debe ser minimizado
- Distancia intra-cluster baja y distancia inter-cluster alta
Índice de Dunn
D = min1 ≤ i ≤ n⎧⎩min1 ≤ j ≤ n, i ≠ j⎧⎩(d(i, j))/(max1 ≤ k ≤ nd’(k))⎫⎭⎫⎭
donde
-
d(i, j) representa la distancia entre clusters i y j
- se pueden usar cualquier número de distancias (por ejemplo, distancia de centroides)
-
d’(k) mide la distancia intra-cluster para el cluster k
- se puede medir de distintas formas (por ejemplo, la distancia maximal entre cualquier par de elementos)
- Algoritmos que producen clusters con alto índice de Dunn son más deseables.
Correlación Cofenética (para dendagramas)
c = ( ⎲⎳i < j(x(i, j) − x)(t(i, j) − t))/(√([ ⎲⎳i < j(x(i, j) − x)2][ ⎲⎳i < j(t(i, j) − t)2]))
donde
- x(i, j) = |Xi − Xj| es la distancia Euclideana común entre los puntos i y j
-
t(i, j) es la distancia dendrogrammatic entre los puntos i y j
- El alto del primer nodo que los une a ambos
- c es el promedio dex(i, j) yt(i, j), respectivamente
Robustez: Partición de muestras
- Partir los datos en dos, al azar
- Hacer el cluster de un grupo y clasificar los elementos del segundo usando los centroides del primero
- Hacer cluster del segundo grupo y extenderlo al primero como antes
- Comparar los dos clusterings, por ejemplo, el índice de Rand
Validación Externa
Si existe un standard con el mismo número exacto de clusters y una correspondecia entre ellos, se puede usar la estadística kappa directamente
- Matriz de Confusión
- Pureza
-
Precision / Recall / F
- F-measure de los pares de conteo (independiente del número de clusters en cada set)
- Coeficiente de Rand / Jaccard
- Hubert’s Γ
Matriz de Confusión
-
Para cada cluster πi (con 1 ≤ i ≤ k) y cluster objetivo πminj (para 1 ≤ j ≤ km), cij = |πi∩πminj|:
- Para cada cluster i, definimos la particiónri el cluster objetivo más parecido al cluster i, entonces
cm(Π) = (m − k⎲⎳i = 1ciri)/(m)
-
0 ≤ cm(Π) < 1 mide el "desacuerdo" entre Π y Πmin
- Si cm(Π) es cerca de 0 son muy parecidos, cerca de 1 son muy distintos.
Pureza
- La pureza p(πi) de clusters πi está dado por p(πi) = max{(ci1)/(|πi|), …, (cikm)/(|πi|)}, donde los ciri están definidos como en la matriz de confusión
- De aquí se desprende que 0 ≤ p(πi) ≤ 1 y que valores altos de p(πi) indican que la mayoría de los puntos en πi vienen del mismo cluster que en la partición óptima
- La pureza total está definida como:
p(Π) = k⎲⎳i = 1(|πi|)/(m)p(πi)
- Cuando km = k, p(π) = 1 − cm(π)
Precision / Recall / F
-
Con una biyección de clusters calculados a clusters óptimos es posible calcular las métricas de recuperación de la información usuales
- Igual que otras métricas de concordancia, como la estadísticaκ
-
Una variación interesante es utilizar la métrica F sobre pares de elementos
- Esta métrica independiente del número de clusters
- Puede ser aplicada a una muestra del conjunto de puntos (no es necesario armar clusters sobre todos los puntos)
Coeficientes de Rand / Jaccard
- Definimos un par (xi⃗, xj⃗) tal que xi⃗ ∈ π ∈ Π y xj⃗ ∈ πmin ∈ Πmin. Sobre conjunto de todos los tales pares podemos definir los siguientes números:
m00
=
|xj⃗∉π, xi⃗∉πmin|
m10
=
|xj⃗ ∈ π, xi⃗∉πmin|
m01
=
|xj⃗∉π, xi⃗ ∈ πmin|
m11
=
|xj⃗ ∈ π, xi⃗ ∈ πmin|
- La estadística de Rand y el coeficiente de Jaccard se definen entonces como:
Estadistica de Rand
=
(m00 + m11)/(m00 + m01 + m10 + m11)
Coeficiente de Jaccard
=
(m11)/(m01 + m10 + m11)
LaΓ de Hubert
Es una métrica de similitud de dos matrices definidas así:
Γ = (1)/(M)N − 1⎲⎳i = 1N⎲⎳j = i + 1X(i, j)Y(i, j)
= ⎡⎣(1)/(M)N − 1⎲⎳i = 1N⎲⎳j = i + 1(X(i, j) − μX)(Y(i, j) − μY)⎤⎦⁄σXσY
dondeX, Y son las matrices a comparar (con media y varianzasμx, μY, σX, σY, respectivamente ), M es el total de puntos y N es el total de clusters
Matrices que se suelen usar:
- La matriz de proximidad (distancia) P
- La matriz de Cluster C(i, j) = {1, si xi, xj pertenecen al mismo cluster, 0 sino}
- La matriz DistanciaQ(i, j) = d(vci, vcj) donde vci, vcj son los centroides de los clusters a los que xi, xj pertenecen.
Rechazando la hipótesis nula
- ¿Y qué pasa cuando los datos no tienen ninguna estructura?
- ¿Cómo sabemos que nuestros clusters no son mejor que clusters tomados al azar?
- Simulaciones Monte Carlo