Aprendizaje Automático sobre
Grandes Volúmenes de Datos

Clase 7

Pablo Ariel Duboue, PhD

Universidad Nacional de Córdoba,
Facultad de Matemática, Astronomía y Física

None.1 Septima Clase: Clustering Estadístico

None.1.1 Clase anterior

Clase pasada:
- Jacob Kogan: Introduction to Clustering Large and High-Dimensional Data (2007)
- Wikipedia: Cluster Analysis (Evaluation of clustering results)
  - http://en.wikipedia.org/wiki/Cluster_analysis#Evaluation_of_clustering_results
- Halkidi, Batistakis & Vazirgiannis: On Clustering Validation Techniques. Journal of Intelligent Information Systems December (2001), Volume 17, Issue 2-3, pp 107-145.
- Everitt, Landau & Leese: Cluster Analysis (2001)
- Capítulo 7 del Owen et al. (2012)
Ésta clase:
- Capítulo 9 del Owen et al. (2012)
- Sección 6.12 del Mitchel (1997)

Preguntas

¿Cómo representar instancias vectorialmente?
- Para más ejemplos ver Capítulo 8 del Owen et al. (2012)
¿Cómo usar los clusters?
- Para más ejemplos ver Capítulo 12 del Owen et al. (2012)
¿Qué método de clustering utilizar? ¿Qué métrica usar para evaluar?
- El dilema de la abundancia
- Para grandes volúmenes de datos
  - Usar K-Means
  - Validación interna: separación usando distancia entre centroides
  - Robustez: separación de muestras

Recordatorio

El sitio Web de la materia es http://aprendizajengrande.net
- Allí está el material del curso (filminas, audio)
Leer la cuenta de Twitter https://twitter.com/aprendengrande es obligatorio antes de venir a clase
- Allí encontrarán anuncios como cambios de aula, etc
- No necesitan tener cuenta de Twitter para ver los anuncios, simplemente visiten la página
Suscribirse a la lista de mail en aprendizajengrande@librelist.com es optativo
- Si están suscriptos a la lista no necesitan ver Twitter
Feedback para alumnos de posgrado es obligatorio y firmado, incluyan si son alumnos de grado, posgrado u oyentes
- El "resúmen" de la clase puede ser tan sencillo como un listado del título de los temas tratados

Revisión K-Means

Se basa en el concepto de elementos sintéticos:
cada cluster se lo representa por un centroide, un elemento ficticio
- en vez de calcular la distancia a todos los elementos del cluster, se la calcula sólo al elemento ficticio
El algoritmo recibe como parámetro el número K de clusters
Al comienzo se toman como centroides K elementos al azar
En cada paso, se re-clasifican los elementos según el centroide al que están más cerca
Para cada cluster, se re-calcula el centroide como la media de los elementos del cluster
- ¿Cómo calcular el centroide? Depende de los datos, igual que la distancia.

K-Means, gráficamente

Primero y segundo paso. Los elementos línea punteado son los centroides.

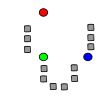
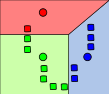
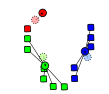
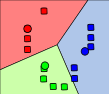
(Wikipedia)

None.1.2 Bigdata

¿Qué es Bigdata?

Es un término comercial
- Sirve para describir productos y servicios relacionados con el manejo de datos
- Según el interés de la persona en vender productos y servicios, son los límites de lo que es bigdata
Es la progresión natural en manejo de datos
- Base de datos
- Datawarehouse
- Soluciones de Bigdata
En el caso del aprendizaje automático, soluciones para grandes volúmenes de datos se utilizan cuando los datos no pueden entrar en la memoria y disco de una sola máquina

El valor está en los datos

Actualmente más y más empresas y particulares se dan cuenta del valor de los datos
El acopio de datos comienza muy antes de la búsqueda de valor en esos datos
Las soluciones de bigdata permiten extraer valor de dichos datos

Las computadoras como humanizadoras

Nací en mediados de los ’70
La mitad de todos los humanos que han existido están vivos en este momento
Ya no es posible el tipo de personalización que es natural para los humanos
El análisis de grandes volúmenes de datos permite el tipo de personalización que nos hace falta

La democratización del cómputo

Algunas ideas inspiradas en la presentación de Alistair Croll durante la semana de Bigdata en Montreal
- http://www.slideshare.net/Tiltmill/cycle-time-trumps-scale-big-data-as-the-organizational-nervous-system-montreal-big-data-week-2014
Computo, lleva a automatizar cosas, las redes llevan a interconectar pero el gran volúmen de datos lleva a predecir y cambiar cosas
Antes había que elegir sólo dos de entre volúmen, velocidad y variedad
- Bibliotecas: gran cantidad de datos variados pero lentas
- Máquina de ordenar monedas: gran cantidad de monedas y rápido pero no son variadas

Los resultados inesperados de la abundancia

Los estudios y algoritmos que estamos usando no son nuevos
- Pero su uso indiscriminado lo es
Antes existían soluciones específicas para grandes volúmenes de datos, a un costo muy elevado
- Censo
- Bancos
Eficiencia ⟹ menores costos ⟹nuevos usos ⟹
⟹mayor demanda ⟹mayor consumo.
- Con más poder de cómputo, las necesidades de procesamiento de grandes volúmenes de datos están disparándose
- La gente tiene necesidad de acceder a tecnología antes reservada para gobiernos y empresas multinacionales

Data Science

Las soluciones de tipo bigdata son interdisciplinarias e involucran:
- Hardware
- Software
- Análisis de datos
Es el surgimiento del profesional especializado en Data Science
La semana que viene vamos a tener una reunión local de profesionales interesados en Data Science, más detalles en @aprendengrande

Conceptos de Bigdata

Algunos conceptos que serán útiles:
- Storage distribuido: para manejar grandes volúmenes de datos, es necesario poder almacenar datos en una red de computadoras
  - El más conocido es HDFS
- Arquitectura de cómputo distribuido: utilizar la red de computadoras de manera eficaz
  - El más mencionado es Hadoop
  - Existe un abanico de soluciones en el sistema Watson usamos ActiveMQ

Pasos del proceso de Bigdata

Adquicisión de datos
Limpieza de datos
Análisis de datos
Uso en predicción

None.1.3 Algoritmo EM

Bayes revisitado

Una hipótesis h define una función sobre los datos. Esta función aproxima la verdadera función que genera los datos f.
La hipótesis de Maximum Likelihood es

h_ML = argmax_h ∈ Hp(D|h)

Si los casos de entrenamiento son mutualmente independientes dado la hipótesis:

h_ML = argmax_h ∈ H∏p(d_i|h)

Si asumimos que los puntos de entrenamiento pertenecen a una distribución Normal con media σ² centrados alrededor del valor de f(x_i) y que los errores son distribuidos con media uniforme entonces (d_i = f(x_i) + e_i)

h_ML = argmax_h ∈ H∏(1)/(√(2πσ²))e^{− (1)/(2σ²)(d_i − μ)²}

Estimador ML

Manipulando algebraicamente y simplificando

h_ML = argmax_h ∈ H∏(1)/(√(2πσ²))e^{− (1)/(2σ²)(d_i − μ)²} = argmax_h ∈ H∏(1)/(√(2πσ²))e^{− (1)/(2σ²)(d_i − h(x_i))²} = argmin_h ∈ H^m⎲⎳_i = 1(d_i − h(x_i))²

Ejemplo de EM

Si observamos datos provenientes de una Gaussiana, podemos obtener su media utilizando la función anterior:

μ_ML = argmin_μ^m⎲⎳_i = 1(x_i − μ)²

¿Pero qué hacemos si los datos provienen de dos Gaussianas?
- Consideramos que tenemos variables ocultas, no observadas
- Cada punto es de la forma ⟨x_i, z_i1, z_i2⟩, z_ij es 1 si la instancia i es generada por la Gaussiana j ó 0 si no.
- Si los z_ij fueran observados, podríamos usar el estimador arriba para calcular h = ⟨μ₁, μ₂⟩
EM
1. Calcular el valor de E[z_ij] asumiendo que h = ⟨μ₁, μ₂⟩ es cierta
2. Calcular una nueva h́ = ⟨μ́₁, μ́₂⟩ asumiendo que losE[z_ij] son correctos

Calculando los E[z_ij]

Si asumimos que la hipótesis h = ⟨μ₁, μ₂⟩ es correcta, entonces

E[z_ij] = (p(x = x_i|μ = μ_i))/(²⎲⎳_n = 1p(x = x_i|μ = μ_n)) = (e^{− (1)/(2σ²)(x_i − μ_j)²})/(²⎲⎳_n = 1e^{− (1)/(2σ²)(x_i − μ_n)²})

Calculando los μ_i

Si asumimos que el valor de las variables ocultas es correcto, entonces

μ_j = (^m⎲⎳_i = 1E[z_ij]x_i)/(^m⎲⎳_i = 1E[z_ij])

None.1.4 Thoughtland

Thoughland

Proyecto actual, 100% Software Libre
Visualizando superficies de error n-dimensionales
- Entrada: datos + algoritmo de aprendizaje automático
- Salida: un párrafo de texto describiendo "como se vé" la superficie del error en n-dimensiones
Aprendizaje automático con Weka (nube de puntos del error vía cross-validación)
Clustering con Apache Mahout (usando clustering basado en modelos)
Generación de texto (usando OpenSchema y SimpleNLG)
http://thoughtland.duboue.net
- Scala
- Open source: https://github.com/DrDub/Thoughtland

Ejemplo de Thoughtland

Entrada

Pequeño dataset, del UCI Machine Learning Repository: http://www.ics.uci.edu/~mlearn/
- Auto MPG: http://archive.ics.uci.edu/ml/machine\-learning-databases/auto-mpg/

@relation auto_mpg

@attribute mpg numeric

@attribute cylinders numeric

@attribute displacement numeric

@attribute horsepower numeric

@attribute weight numeric

@attribute acceleration numeric

@attribute modelyear numeric

@attribute origin numeric

@data

18.0,8,307.0,130.0,3504.,12.0,70,1

14.0,8,455.0,225.0,3086.,10.0,70,1

24.0,4,113.0,95.00,2372.,15.0,70,3

22.0,6,198.0,95.00,2833.,15.5,70,1

...

+400 instancias más

Salida

MLP, 2 capas ocultas (3, 2 neuronas), acc. 65%:

There are four components and eight dimensions. Components One, Two and Three are small. Components One, Two and Three are very dense. Components Four, Three and One are all far from each other. The rest are all at a good distance from each other.

MLP, 1 capas ocultas (8 neuronas), acc. 65.7%:

There are four components and eight dimensions. Components One, Two and Three are small. Components One, Two and Three are very dense. Components Four and Three are far from each other. The rest are all at a good distance from each other.

MLP, 1 capas ocultas (1 neurona), acc. 58%:

There are five components and eight dimensions. Components One, Two and Three are small and Component Four is giant. Components One, Two and Three are very dense. Components One and Four are at a good distance from each other. Components Two and Three are also at a good distance from each other. Components Two and Five are also at a good distance from each other. The rest are all far from each other.

Arquitectura

Aprendizaje Automático

La función de error se computa como el error en cada punto de entrada
Para una clase numérica y un caso de entrenamiento (x⃗, y), e = ∥f(x⃗) − y∥
- f se entrena en un fold que no contiene a x⃗ (cros-validación)
Para clase nominal se utiliza 1 si la clase es diferente y 0 si es la misma

Clustering

Se identifican clusters en la nube de puntos de error usando una mezcla de modelos de Dirichlet
- Implementado en Apache Mahout
- Tiene una interpretación geométrica como esferoides n-dimensionales
Algunas features de entrada presentan agrupamientos naturales de los datos que opacan los clusters obtenidos sobre la función de error
- Los valores de la función de error se re-escalan para que tengan más prominencia

Aprendizaje Automático sobre Grandes Volúmenes de Datos