Aprendizaje Automático sobre
Grandes Volúmenes de Datos

Clase 8

Pablo Ariel Duboue, PhD

Universidad Nacional de Córdoba,
Facultad de Matemática, Astronomía y Física

None.1 Octava Clase: Recomendación

None.1.1 Clase anterior

Material de lectura

Clase pasada:
- Capítulo 9 del Owen et al. (2012)
- Sección 6.12 del Mitchel (1997)
Ésta clase:
- Capítulo 2 y 4 del Owen et al. (2012)

Preguntas

EM y k-Means
- EM es mucho más general que k-Means
- Estimar variables ocultas relacionadas con variables observadas
- Converge a maximos locales
Thoughtland y aprendizaje automático
- Los textos generados por Thoughtland son basados en características matemáticas (densidad, tamaño, en algún momento incorporaremos otras características como convexidad)
- La generación de textos no utiliza aprendizaje automático

Recordatorio

El sitio Web de la materia es http://aprendizajengrande.net
- Allí está el material del curso (filminas, audio)
Leer la cuenta de Twitter https://twitter.com/aprendengrande es obligatorio antes de venir a clase
- Allí encontrarán anuncios como cambios de aula, etc
- No necesitan tener cuenta de Twitter para ver los anuncios, simplemente visiten la página
Suscribirse a la lista de mail en aprendizajengrande@librelist.com es optativo
- Si están suscriptos a la lista no necesitan ver Twitter
Feedback para alumnos de posgrado es obligatorio y firmado, incluyan si son alumnos de grado, posgrado u oyentes
- El "resúmen" de la clase puede ser tan sencillo como un listado del título de los temas tratados

Revisión EM

Una hipótesis h define una función sobre los datos. Esta función aproxima la verdadera función que genera los datos f.
La hipótesis de Maximum Likelihood es

h_ML = argmax_h ∈ Hp(D|h)

Si los casos de entrenamiento son mutualmente independientes dado la hipótesis:

h_ML = argmax_h ∈ H∏p(d_i|h)

Si asumimos que los puntos de entrenamiento pertenecen a una distribución Normal con media σ² centrados alrededor del valor de f(x_i) y que los errores son distribuidos con media uniforme entonces (d_i = f(x_i) + e_i)

h_ML = argmax_h ∈ H∏(1)/(√(2πσ²))e^{− (1)/(2σ²)(d_i − μ)²}

Estimador ML

Manipulando algebraicamente y simplificando

h_ML = argmax_h ∈ H∏(1)/(√(2πσ²))e^{− (1)/(2σ²)(d_i − μ)²} = argmax_h ∈ H∏(1)/(√(2πσ²))e^{− (1)/(2σ²)(d_i − h(x_i))²} = argmin_h ∈ H^m⎲⎳_i = 1(d_i − h(x_i))²

Ejemplo de EM

Si observamos datos provenientes de una Gaussiana, podemos obtener su media utilizando la función anterior:

μ_ML = argmin_μ^m⎲⎳_i = 1(x_i − μ)²

¿Pero qué hacemos si los datos provienen de dos Gaussianas?
- Consideramos que tenemos variables ocultas, no observadas
- Cada punto es de la forma ⟨x_i, z_i1, z_i2⟩, z_ij es 1 si la instancia i es generada por la Gaussiana j ó 0 si no.
- Si los z_ij fueran observados, podríamos usar el estimador arriba para calcular h = ⟨μ₁, μ₂⟩
EM
1. Calcular el valor de E[z_ij] asumiendo que h = ⟨μ₁, μ₂⟩ es cierta
2. Calcular una nueva h́ = ⟨μ́₁, μ́₂⟩ asumiendo que losE[z_ij] son correctos

Calculando los E[z_ij]

Si asumimos que la hipótesis h = ⟨μ₁, μ₂⟩ es correcta, entonces

E[z_ij] = (p(x = x_i|μ = μ_i))/(²⎲⎳_n = 1p(x = x_i|μ = μ_n)) = (e^{− (1)/(2σ²)(x_i − μ_j)²})/(²⎲⎳_n = 1e^{− (1)/(2σ²)(x_i − μ_n)²})

Calculando los μ_i

Si asumimos que el valor de las variables ocultas es correcto, entonces

μ_j = (^m⎲⎳_i = 1E[z_ij]x_i)/(^m⎲⎳_i = 1E[z_ij])

None.1.2 Recomendación

Collaborative Filtering

Filtrar información usando comunidades de personas
Usuarios, ítems y preferencias
- Pablo, http://aprendizajengrande.net, 1.0
- Pablo, http://duboue.net, 5.0
- Pablo, http://google.com, 2.0
- Juan, http://aprendizajengrande.net, 3.0
- Juan, http://getyatel.org, 5.0
- Juan, http://google.com, 1.0
- John, http://google.com, 3.0
- John, http://cnn.com, 5.0
- John, http://nba.com, 3.0

Recomendación basada en Usuarios

para cada ítem i para el cual el usuario u no tiene preferencia:
- para cada otro usuario v que tiene preferencia por i:
  - calcular la similitud s entre u y v
  - acumular la preferencia de v por i, pesada por s
devolver los ítems con mayor preferencia pesada

Vecindad de Usuarios

Para acotar el tiempo de computo del algoritmo anterior, en vez de iterar sobre todos los otros usuarios, definimos una métrica sobre ellos y consideramos sólo los usuarios más cercanos
- O bien los k usuarios más cercanos
- O bien los usuarios cercanos a un cierto nivel máximo de distancia

Métricas de similitud de Usuarios

Euclideana
Tanimoto
- Ignora el valor de las preferencias
- Considera el conjunto de ítems sobre los que los dos usuarios han expresado preferencias
- Tamaño de la intersección dividido la unión
Log-likelihood
- Similar a Tanimoto
- Incorpora el concepto de concordancia por chance
- Similar a la estadística κ
  - A dos personas les gustan un mismo ítem porque es popular no porque sean parecidas

Métricas de similitud de Usuarios

Coeficiente de correlación Pearson
- Un número entre -1 y 1 que mide la tendencia de dos series de números, tomados de a pares, de moverse al unísono
- Covarianza normalizada por la varianza
- Sólo se puede computar para ítems donde ambos usuarios han expresado preferencias
- Similitud por coseno cuando los vectores están centrados
Valores posicionales y el Coeficiente de correlación de Spearman
- En vez de usar los valores de las preferencias, usar la diferencia relativa posicional
- Reemplazar los valores de preferencias por su posición y aplicar Pearson

Inferencia de Preferencias

Como en aprendizaje supervisado, es posible completar datos faltantes para mejorar las métricas de similitud
- Las estrategias que vimos en ingeniería de features pueden ser usadas
No ayuda mucho en la práctica
Enlentece mucho los algoritmos presentados

Recomendación basada en Ítems

para cada ítem i para el cual el usuario u no tiene preferencia:
- para cada ítem j que u tiene una preferencia:
  - calcular la similitud s entre i y j
  - acumular la preferencia de u por j, pesada por s
devolver los ítems con mayor preferencia pesada

Interpretación Matricial

Matriz de co-ocurrencia

	i₁	i₂	i₃	i₄	i₅
i₁	5	2	1	3	4
i₂		3	1	2	3
i₃			4	2	2
i₄				1	1
i₅					7

Vector de preferencia (uno por usuario)

i₁	i₂	i₃	i₄	i₅
5	2	1	3	4

Algoritmo Pendiente-uno

Cuando dos personas tienen preferencias por dos ítems, es posible que haya una tendencia clara de la diferencia de preferencias entre los dos
Off-line: calcular la diferencia promedio entre ítems
On-line: igual que basado en ítems pero usar la diferencia promedio en la acumulación

None.1.3 Cierra Aprendizaje Automático

Resúmen

Features, proceso de aprendizaje automático
Aprendizaje Supervisado
Aprendizaje No Supervisado
Recomendación

Naive Bayes

Teorema de Bayes

P(y|f⃗) = (P(f⃗|y)P(y))/(P(f⃗))

Naive Bayes asume que las features son probabilisticamente independientes

y_NB = max_yP(f₁, ..., f_n|y)P(y) = max_yP(f₁|y)...P(f_n|y)P(y)

Podemos estimar P(f_i|y) a partir de conteos

NB: de conteos a probabilidades

Conteos de instancias (N_i) vs. conteos de features (N_f)
De la definición de probabilidad conjunta:
P(".com"|Arts)P(Arts) = P(".com", Arts) = (N_f(".com", Arts))/(N_f(.))
De la definición de probabilidad simple:
P(Arts) = (N_i(Arts))/(N_i(.))
Despejando para la probabilidad condicional:
P(".com"|Arts) = (N_i(.))/(N_f(.))(N_f(".com", Arts))/(N_i(Arts))

Árboles de Decisión

Dividir los datos según un feature solo y un predicado simple sobre ese feature

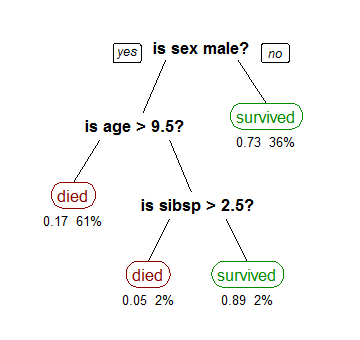
(CC-BY-SA Stephen Milborrow, from Wikipedia)

ID3

ID3 (Ejemplos, Clase Objetivo, Features)

Crear un nodo raíz

Si todos los ejemplos son positivos, devolver la raíz con clase +

Si todos los ejemplos son negativos, devolver la raíz con clase -

Si no quedan features, devolver la raíz con clase igual al valor más común

Caso contrario

A ← la feature que mejor clasifica los ejemplos
El feature en la raíz es A
Para cada valor posible v_i del feature A

Agregar rama al árbol bajo la raíz (testeo A=v_i)
Sean Ejemplos(v_i) el subconjunto de los ejemplos que tienen v_i para A
Si Ejemplos(v_i) está vacío, para esta rama setear la clase al valor objetivo más común
Sino agregar un subárbol ID3 (Ejemplos(v_i), Clase Objetivo, Features– {A})

Devolver la raíz

Information Gain

Podemos definir Information Gain a partir de la entropía (qué tan "ruidosa" es la partición)
En caso de una partición binaria:

Entropy(S) = − p₊log₂(p₊) − p₋log₂(p₋)

Múltiples categorías (m):

Entropy(S) = ^m⎲⎳_i = 1 − p_ilog₂p_i

Ganancia de información entonces es:

Gain(S, A) = Entropy(S) − ⎲⎳_{v ∈ valores(A)}(|S_v|)/(|S|)Entropy(S_v)

K-Means

Se basa en el concepto de elementos sintéticos:
- cada cluster se lo representa por un centroide, un elemento ficticio
- en vez de calcular la distancia a todos los elementos del cluster, se la calcula sólo al elemento ficticio
El algoritmo recibe como parámetro el número K de clusters
Al comienzo se toman como centroides K elementos al azar
En cada paso, se re-clasifican los elementos según el centroide al que están más cerca
Para cada cluster, se re-calcula el centroide como la media de los elementos del cluster
- ¿Cómo calcular el centroide? Depende de los datos, igual que la distancia